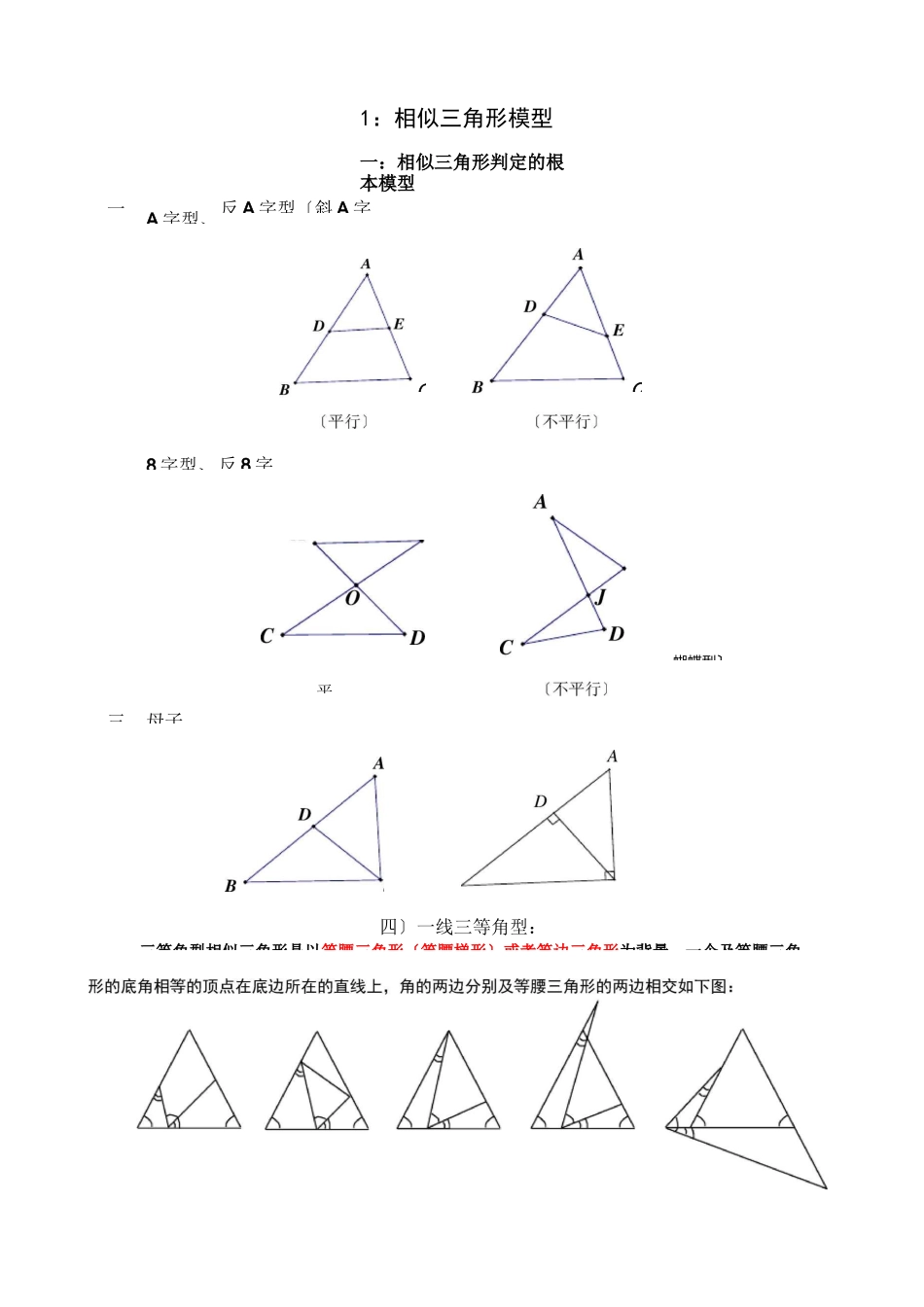
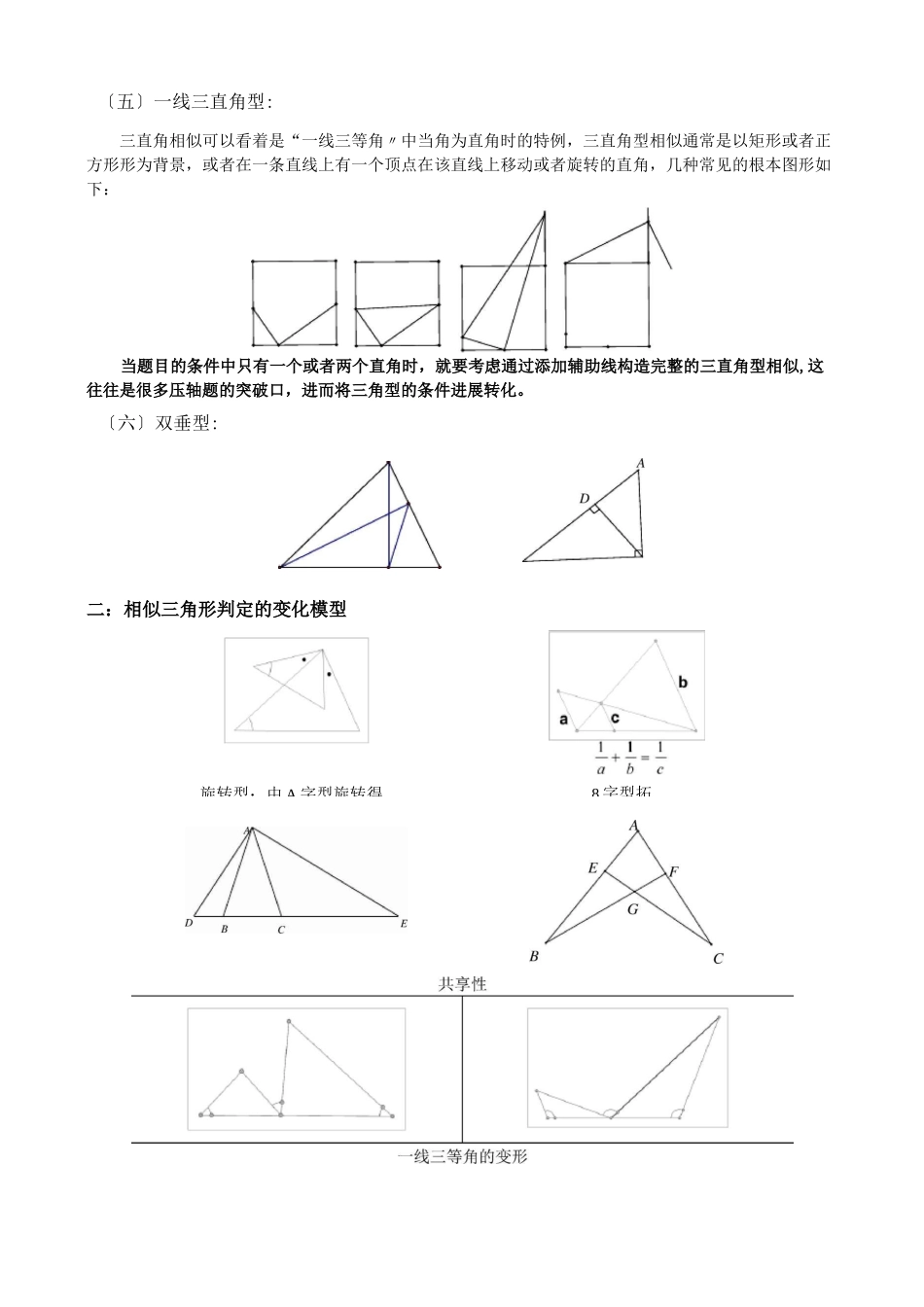
一A 字型、反 A 字型〔斜 A 字三8 字型、反 8 字蝴蝶型〕母子1:相似三角形模型一:相似三角形判定的根本模型四〕一线三等角型:CC平三等角型相似三角形是以等腰三角形〔等腰梯形〕或者等边三角形为背景,一个及等腰三角旋转型:由 A 字型旋转得8 字型拓〔五〕一线三直角型:三直角相似可以看着是“一线三等角〃中当角为直角时的特例,三直角型相似通常是以矩形或者正方形形为背景,或者在一条直线上有一个顶点在该直线上移动或者旋转的直角,几种常见的根本图形如下:当题目的条件中只有一个或者两个直角时,就要考虑通过添加辅助线构造完整的三直角型相似,这往往是很多压轴题的突破口,进而将三角型的条件进展转化。〔六〕双垂型:二:相似三角形判定的变化模型一线三直角的变形2:相似三角形典型例题〔1〕母子型相似三角形例 1:如图,梯形 ABCD 中,AD〃BC,对角线 AC、BD 交于点 O,BE〃CD 交 CA 延长线于 E.求证:OC2=OA°OE.例 2::如图,△ABC 中,点 E 在中线 AD 上,ZDEB=ZABC.求证:⑴ DB2=DE-DA;⑵ ZDCE=ZDAC.例 3::如图,等腰△ABC 中,AB=AC,AD 丄 BC 于 D,CG〃AB,BG 分别交 AD、AC 于 E、F.求证:BE2二 EF°EG.1、如图,AD 为 AABC 的角平分线,EF 为 AD 的垂直平分线.求证:FD2二 FB°FC.2、AD 是 RtAABC 中 ZA 的平分线,ZC=90。,EF 是 AD 的垂直平分线交 AD 于 M,EF、BC 的延长线交于一点 N。求证:(l)AAMEs^NMD;(2)ND2=NC・NB3、如图,在△ABC中,求证:EB・ZACB=90°,CD 丄 AB 于 D,E 是 AC 上一点,CF 丄 BE 于 F。4.在 AABC中,AB=AC,高 AD 及 BE 交于 H,EFC,垂足为 F,延长 AD 至 l」G,使 DG=EF,M 是 AH 的中点。求证:ZGBM=90。BG2〕双垂型1、如图,在△ABC 中,ZA=60。,BD、CE 分别是 AC、AB 上的高求证:〔1〕△ABDs^ACE;〔2〕△ADE^^ABC;(3)BC=2ED2、如图,锐角△ABC,AD、CE 分别是 BC、AB 边上的高,△ABC 和△BDE 的面积分别是 27 和 3,DE=6\迈,1、△ABC 是等边三角形,DBCE 在一条直线上,ZDAE=120°,BD=1,CE=3,求等边三角形的边长.2、:如图,在 RtAABC 中,AB=AC,ZDAE=45°.求证:〔1〕△ABEs^ACD;〔2〕BC2=2BE-CD.3〕共A点 B 重合〕且保持 ZAPQ=ZABC.① 假设点 P 在线段 CB 上〔如图〕且 BP=6,求线段 CQ 的长;② 假设 BP=x,CQ=y,求 y 及 x之间的函数关系式,并写出函数的定义域;...