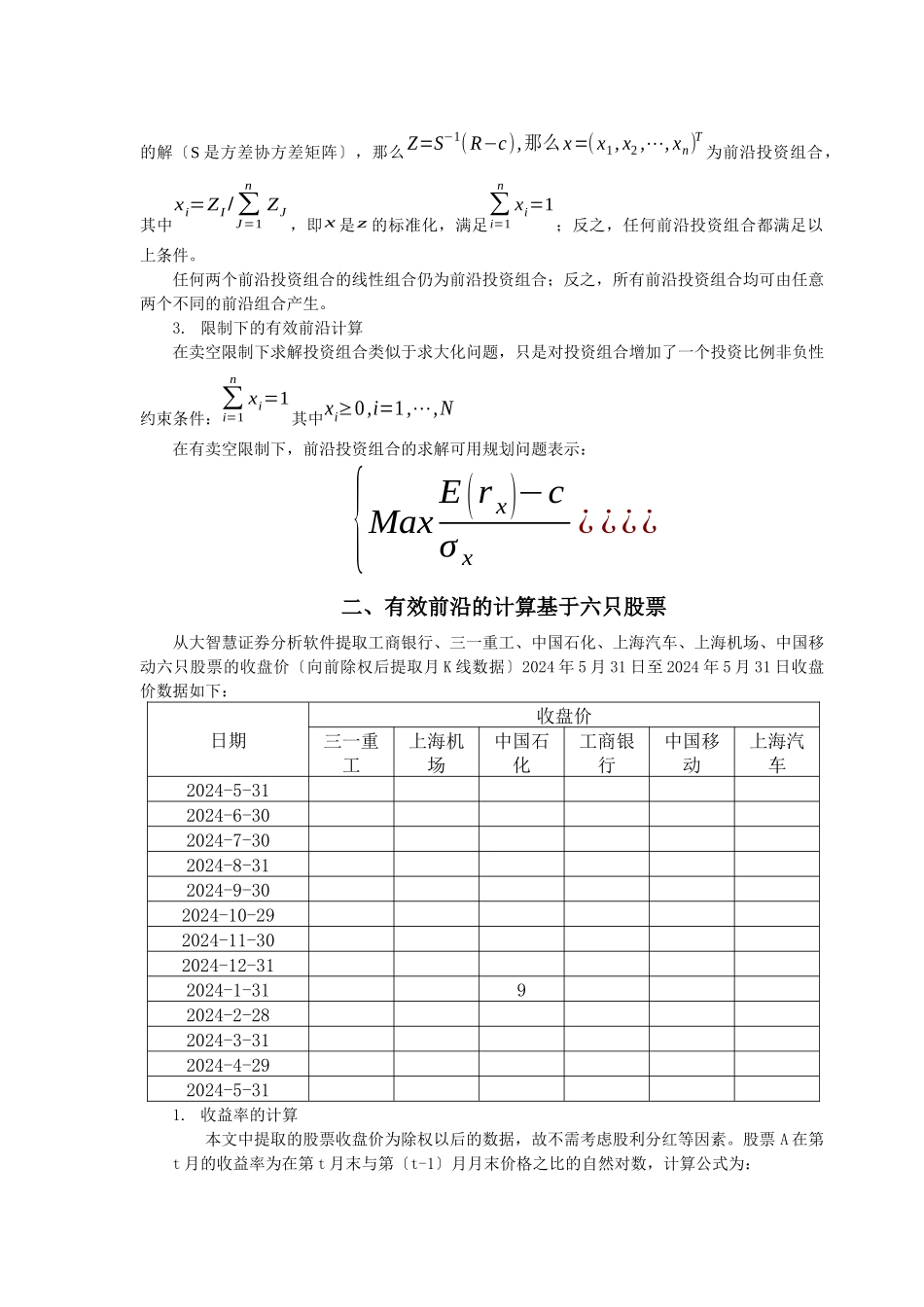
有 、 无 卖 空 限 制 下 有 效 前 沿 的 计 算——基于股票案例的讨论 [摘要]在丰富的金融投资理论中,投资组合理论占有非常重要的地位,金融产品本质上市各种金融工具的组合。现代投资组合理论试图解释获得最大投资收益与防止过风险之间的根本权衡关系,也就是说投资者将不同的投资品种按一定的比例组合在一起作为投资对象,以到达在保证预订收益的前提下把风险降到最小或者在一定风险的前提下使收益率最大。在中国股市上运用马科维茨模型讨论投资有限前沿组合,探究风险变动规律,从而知道各股票投资组合在到达最正确时所占的比例。[关键词] 马科维茨模型 投资组合 有效前沿投资者很早就认识到了分散的将资金进行投资可以降低投资风险,扩大投资收益。但在第一个对此问题做出实质性分析的是美国经济学家马科维茨。1952 年马科维茨发表了?证券投资组合选择?,标志着证券组合理论的正式诞生。马科维茨根据每一张证券的预期收益率、方差和所有证券间的协方差矩阵,得到证券组合的有效边界,再根据投资者的效用无差异曲线,确定最正确投资组合。马科维茨的证券组合理论在计算投资组合的收益和方差时非常精确。本文通过对在上交所上市的六只股票运用马科维茨模型进行分析,找到给定风险下的最正确投资组合。一、模型理论经典马科维茨均值-方差模型为:{minσp2=XT∑X¿{maxE(rp)=XTR¿¿¿¿其中R=(R1, R2,⋯Rn)T; Ri=E (ri)是第 i 种资产的预期收益率;X=(x1, x2,⋯, xn)T是投资组合的权重向量;∑ ¿(σij)n×n 是 n 中资产间的协方差矩阵;E (r P)σ和p2分别是投资组合的期望回报率和方差。马科维茨模型以期望收益率期望度量收益,以收益率方差度量风险。在本文中以股票的历史收益率的句子作为期望收益率,可能会造成“追涨的效果〞,在实际中这些收益率可能会不一样;在计算组合风险值时协方差对结果影响较大,在本文中以股票的历史收益率的协方差度量资产风险与相关性,可能会与实际协方差矩阵存在一定的偏差。1.前沿的计算马科维茨均值-方差模型为典型的带约束的二次规划问题,在给定的期望收益时,方差最小解唯一,函数如下:{minσ p2=XT∑ X ¿¿¿¿¿给定计算相应风险最小的组合,即得到有效前沿上一点〔有效组合〕,给定一系列可以有效描绘出有效前沿。有效边界是组合证券资产选择的重要根底。根据 Markwitz 创立的现代证券投资组合理论, 理性的投资者应具有“非满足性〞和“风险回避〞两个特征,...