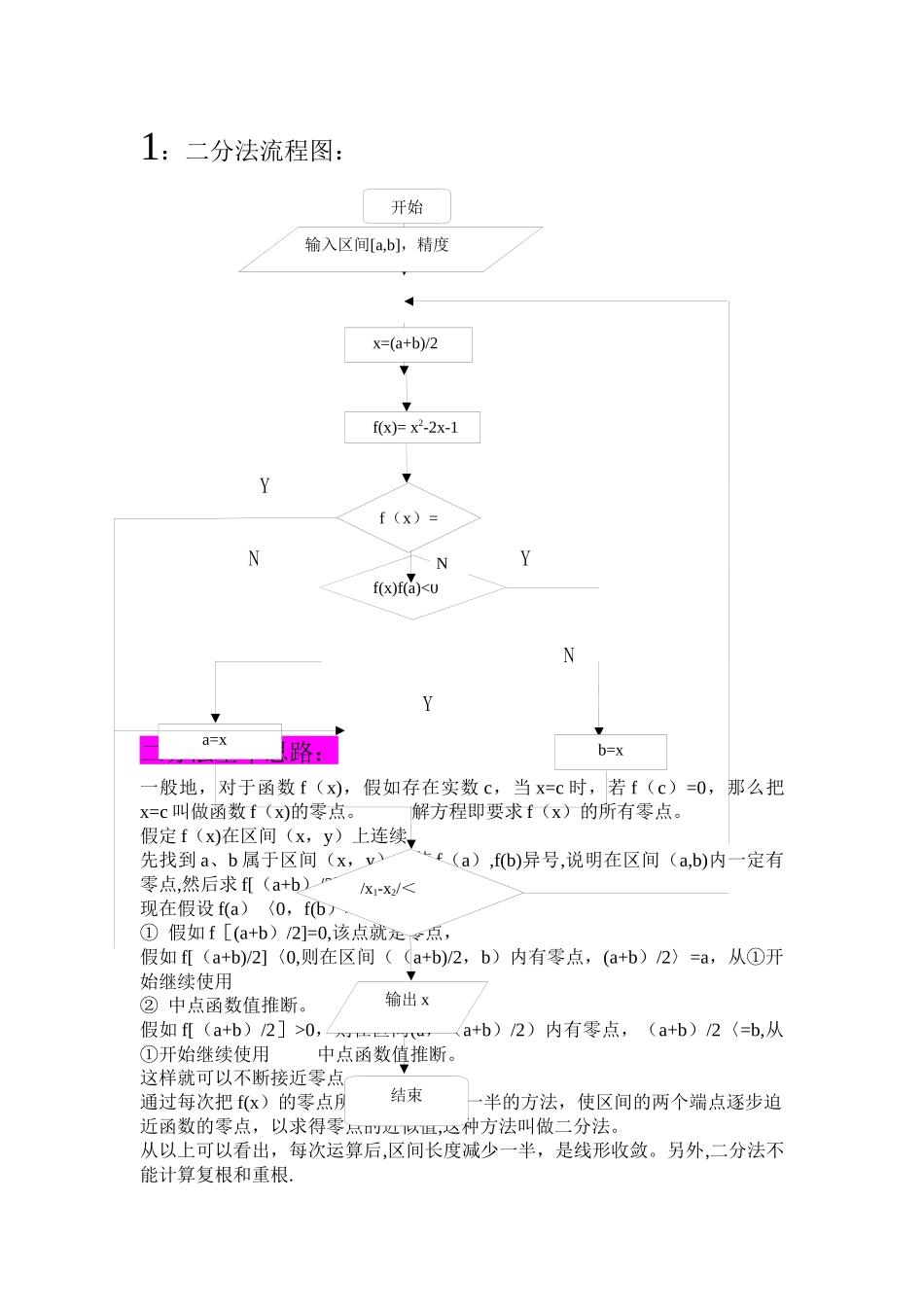
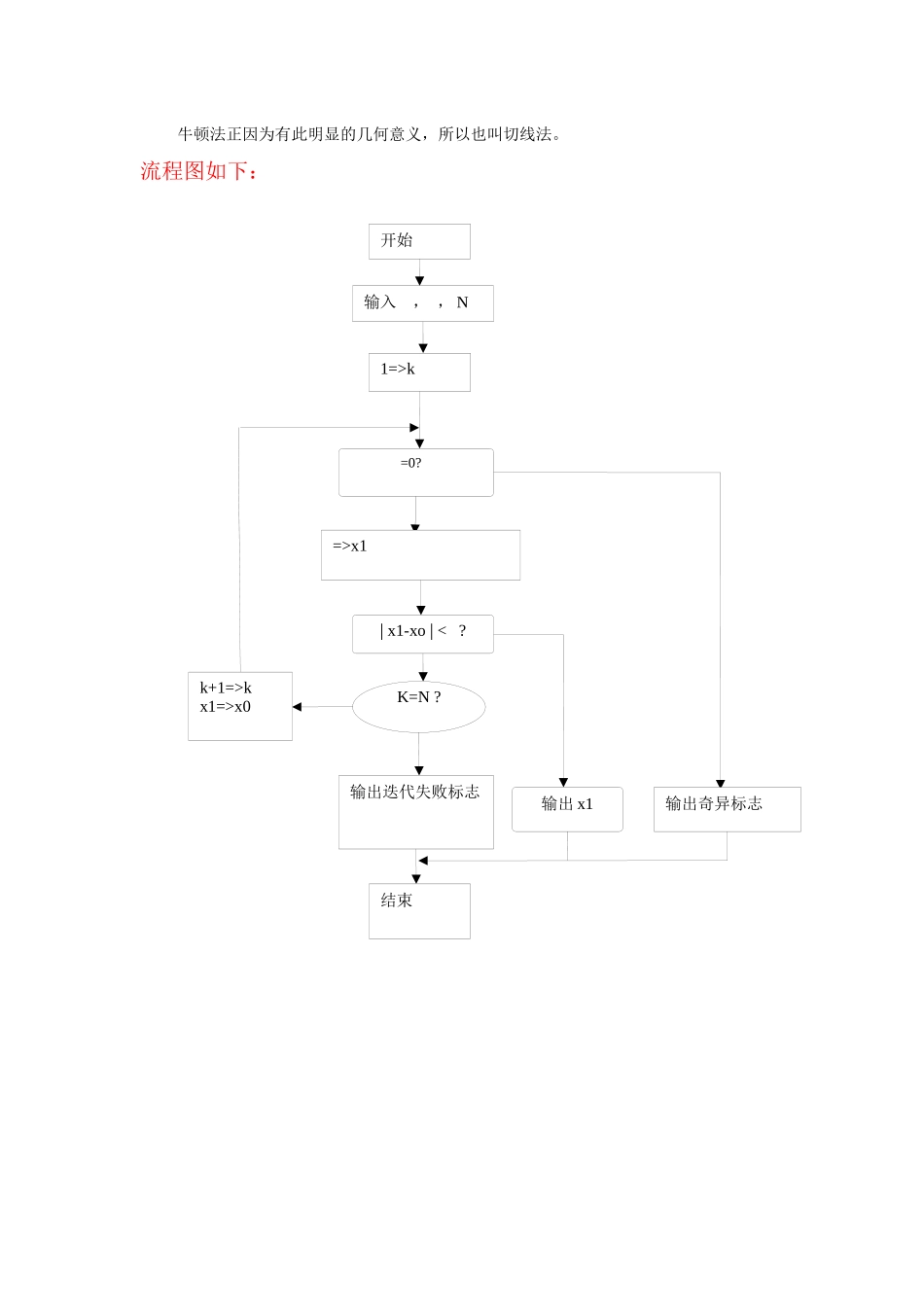
1:二分法流程图: Y N Y N Y 二分法基本思路:一般地,对于函数 f(x),假如存在实数 c,当 x=c 时,若 f(c)=0,那么把x=c 叫做函数 f(x)的零点。 解方程即要求 f(x)的所有零点。 假定 f(x)在区间(x,y)上连续 先找到 a、b 属于区间(x,y),使 f(a),f(b)异号,说明在区间(a,b)内一定有零点,然后求 f[(a+b)/2], 现在假设 f(a)〈0,f(b)>0,a〈b ① 假如 f[(a+b)/2]=0,该点就是零点, 假如 f[(a+b)/2]〈0,则在区间((a+b)/2,b)内有零点,(a+b)/2〉=a,从①开始继续使用 ② 中点函数值推断。 假如 f[(a+b)/2]>0,则在区间(a,(a+b)/2)内有零点,(a+b)/2〈=b,从①开始继续使用 中点函数值推断。 这样就可以不断接近零点. 通过每次把 f(x)的零点所在小区间收缩一半的方法,使区间的两个端点逐步迫近函数的零点,以求得零点的近似值,这种方法叫做二分法。 从以上可以看出,每次运算后,区间长度减少一半,是线形收敛。另外,二分法不能计算复根和重根.开始输入区间[a,b],精度x=(a+b)/2f(x)= x2-2x-1f(x)f(a)<0b=xa=x/x1-x2/<输出 x结束f(x)=0N二分法步骤:用二分法求方程的根的近似值的步骤① 若对于有,则在内至少有一个根。② 取的中点计算③ 若则是的根,停止计算,运行后输出结果若则在内至少有一个根。取;若,则取;④ 若(为预先给定的要求精度)退出计算,运行后输出结果,反之,返回步骤 1,重复步骤 1,2,3二分法 Mtalab 程序syms x; fun=input(’(输入函数形式)fx='); a=input('(输入二分法下限)a=’); b=input(’(输入二分法上限)b=’); d=input('输入误差限 d=’)%二分法求根 %f=inline(x^2—4*x+4); %修改需要求解的 inline 函数的函数体 f=inline(fun);%修改需要求解的 inline 函数的函数体 e=b-a; k=0 ; while e〉d c=(a+b)/2; if f(a)*f(c)〈0 b=c; elseif f(a)*f(c)>0 a=c; else a=c;b=c end e=e/2; k=k+1; end x=(a+b)/2; x%x 为答案 k%k 为次数2,牛顿法及流程图:方程 f(x)=0 的根就是曲线 y=f(x)与 x 轴交点的横坐标 x*,当初始近似值 x0 选取后,过( x0,f(x0))作切线,其切线方程为:y— f(x0)=f′(x0)(x-x0)它与 x 轴交点的横坐标为 x一般地,设 是 x*的第 n 次近似值,过( x,f(x))作 y=f(x)的切线,其切线与 x 轴交点的横坐标...