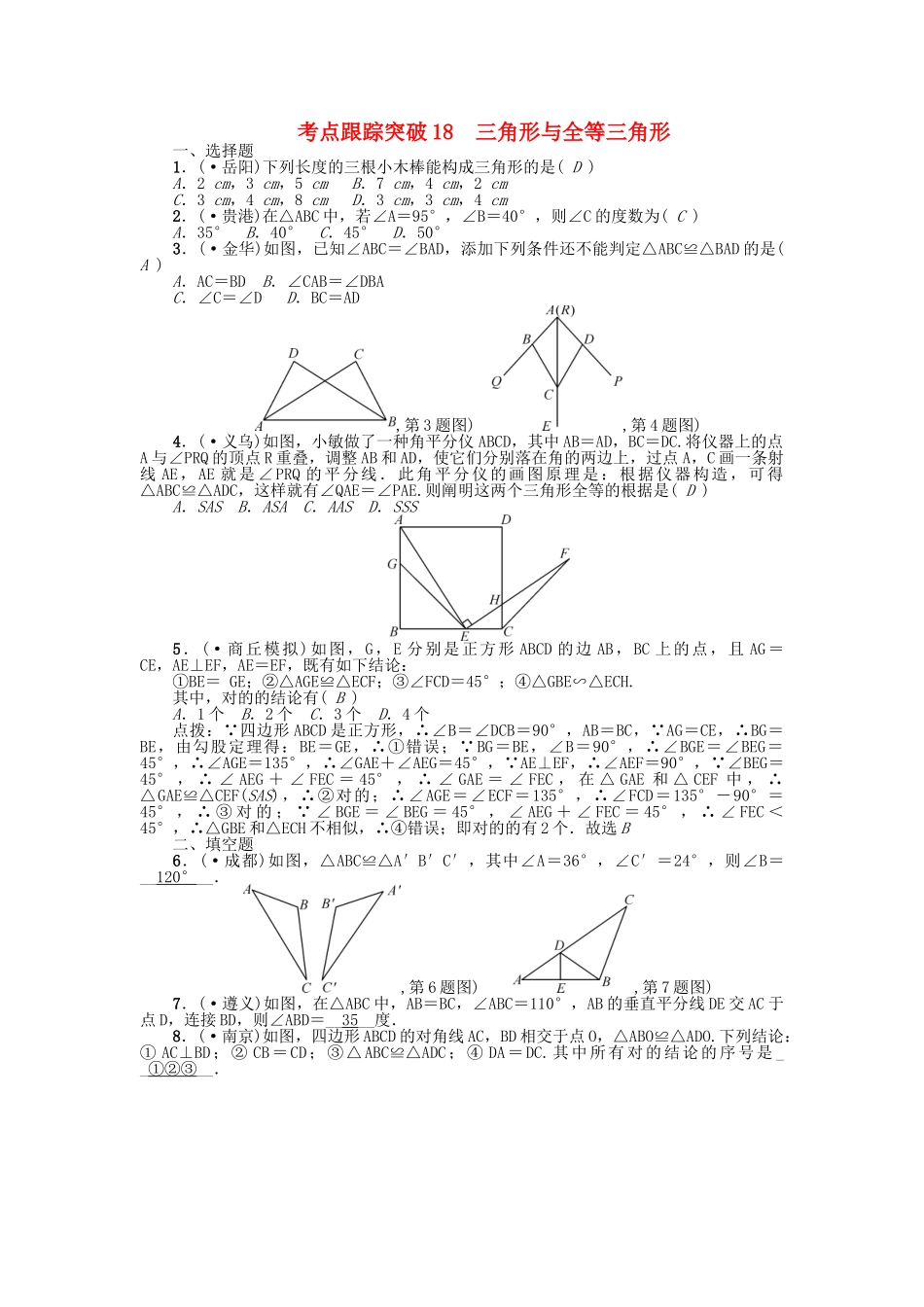
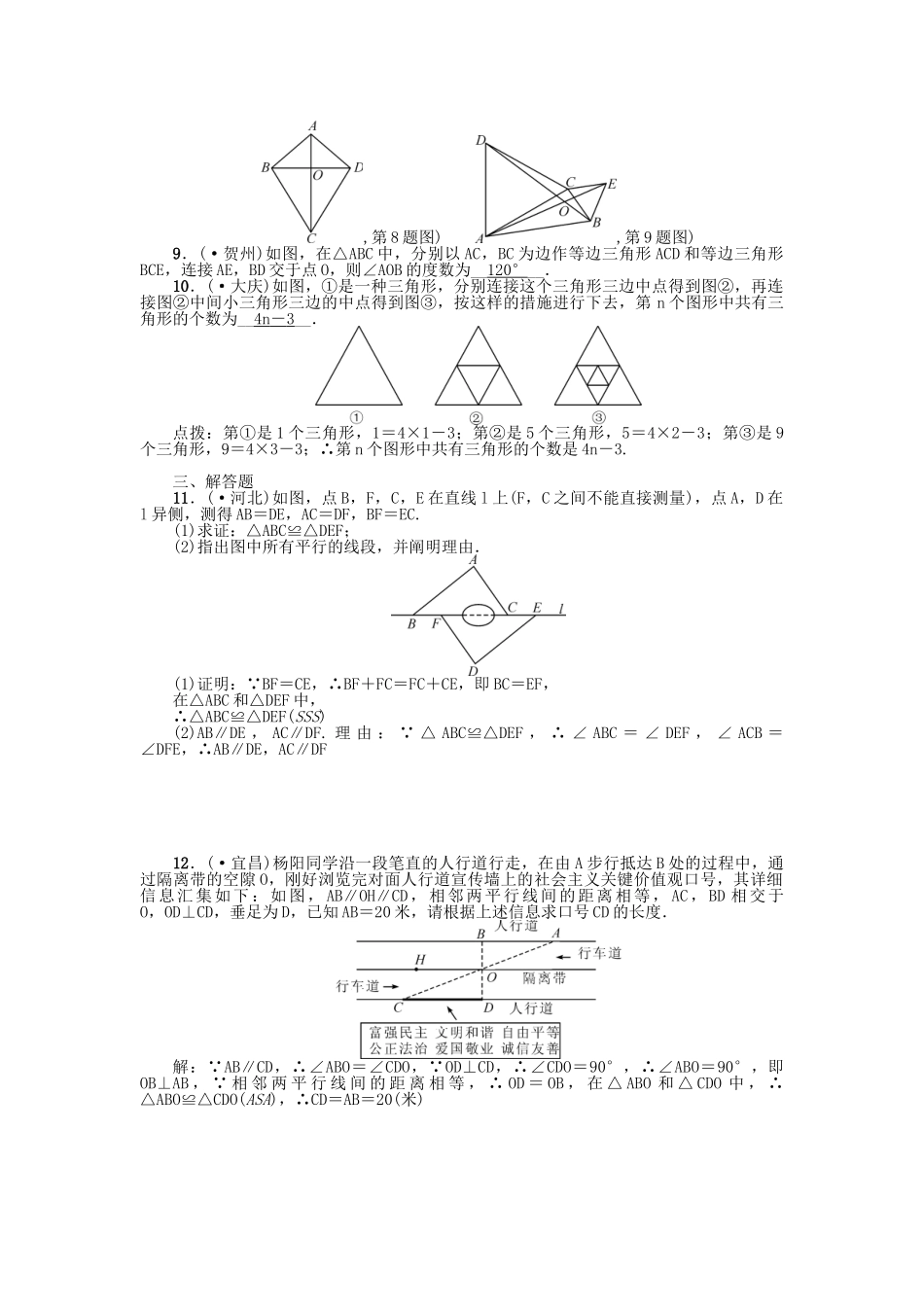
考点跟踪突破 18 三角形与全等三角形一、选择题1.(·岳阳)下列长度的三根小木棒能构成三角形的是( D )A.2 cm,3 cm,5 cm B.7 cm,4 cm,2 cmC.3 cm,4 cm,8 cm D.3 cm,3 cm,4 cm2.(·贵港)在△ABC 中,若∠A=95°,∠B=40°,则∠C 的度数为( C )A.35° B.40° C.45° D.50°3.(·金华)如图,已知∠ABC=∠BAD,添加下列条件还不能判定△ABC≌△BAD 的是( A )A.AC=BD B.∠CAB=∠DBAC.∠C=∠D D.BC=AD,第 3 题图) ,第 4 题图)4.(·义乌)如图,小敏做了一种角平分仪 ABCD,其中 AB=AD,BC=DC.将仪器上的点A 与∠PRQ 的顶点 R 重叠,调整 AB 和 AD,使它们分别落在角的两边上,过点 A,C 画一条射线 AE,AE 就是∠PRQ 的平分线.此角平分仪的画图原理是:根据仪器构造,可得△ABC≌△ADC,这样就有∠QAE=∠PAE.则阐明这两个三角形全等的根据是( D )A.SAS B.ASA C.AAS D.SSS5.(·商丘模拟)如图,G,E 分别是正方形 ABCD 的边 AB,BC 上的点,且 AG=CE,AE⊥EF,AE=EF,既有如下结论:①BE= GE;②△AGE≌△ECF;③∠FCD=45°;④△GBE∽△ECH.其中,对的的结论有( B )A.1 个 B.2 个 C.3 个 D.4 个点拨: 四边形 ABCD 是正方形,∴∠B=∠DCB=90°,AB=BC, AG=CE,∴BG=BE,由勾股定理得:BE=GE,∴①错误; BG=BE,∠B=90°,∴∠BGE=∠BEG=45°,∴∠AGE=135°,∴∠GAE+∠AEG=45°, AE⊥EF,∴∠AEF=90°, ∠BEG=45° , ∴ ∠ AEG + ∠ FEC = 45° , ∴ ∠ GAE = ∠ FEC , 在 △ GAE 和 △ CEF 中 , ∴△GAE≌△CEF(SAS),∴②对的;∴∠AGE=∠ECF=135°,∴∠FCD=135°-90°=45° , ∴ ③ 对 的 ; ∠ BGE = ∠ BEG = 45° , ∠ AEG + ∠ FEC = 45° , ∴ ∠ FEC <45°,∴△GBE 和△ECH 不相似,∴④错误;即对的的有 2 个.故选 B二、填空题6.(·成都)如图,△ABC≌△A′B′C′,其中∠A=36°,∠C′=24°,则∠B=__120°__.,第 6 题图) ,第 7 题图)7.(·遵义)如图,在△ABC 中,AB=BC,∠ABC=110°,AB 的垂直平分线 DE 交 AC 于点 D,连接 BD,则∠ABD=__35__度.8.(·南京)如图,四边形 ABCD 的对角线 AC,BD 相交于点 O,△ABO≌△ADO.下列结论:① AC⊥BD;② CB=CD;③△ABC...