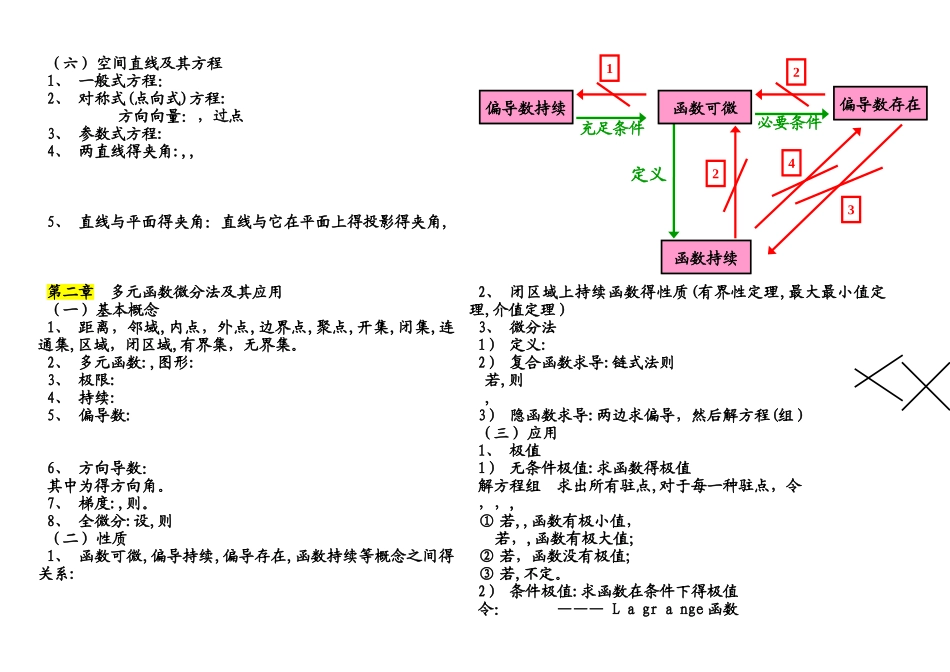
微积分下册知识点第一章 空间解析几何与向量代数(一)向量及其线性运算1、 向量,向量相等,单位向量,零向量,向量平行、共线、共面;2、 线性运算:加减法、数乘;3、 空间直角坐标系:坐标轴、坐标面、卦限,向量得坐标分解式;4、 运用坐标做向量得运算:设,,则 , ; 5、 向量得模、方向角、投影:1) 向量得模:;2) 两点间得距离公式:3) 方向角:非零向量与三个坐标轴得正向得夹角4) 方向余弦:5) 投影:,其中为向量与得夹角。(二)数量积,向量积1、 数量积:1)2)2、 向量积:大小:,方向:符合右手规则1)2)运算律:反互换律 (三)曲面及其方程1、 曲面方程得概念:2、 旋转曲面:面上曲线,绕轴旋转一周:绕轴旋转一周:3、 柱面:表达母线平行于轴,准线为得柱面4、 二次曲面(不考)1) 椭圆锥面:2) 椭球面:旋转椭球面:3) 单叶双曲面:4) 双叶双曲面:5) 椭圆抛物面:6) 双曲抛物面(马鞍面):7) 椭圆柱面:8) 双曲柱面:9) 抛物柱面:(四)空间曲线及其方程1、 一般方程:2、 参数方程:,如螺旋线:3、 空间曲线在坐标面上得投影,消去,得到曲线在面上得投影(五)平面及其方程1、 点法式方程: 法向量:,过点2、 一般式方程:截距式方程:3、 两平面得夹角:,, 4、 点到平面得距离:(六)空间直线及其方程1、 一般式方程:2、 对称式(点向式)方程: 方向向量:,过点3、 参数式方程:4、 两直线得夹角:,, 5、 直线与平面得夹角:直线与它在平面上得投影得夹角, 第二章 多元函数微分法及其应用(一)基本概念1、 距离,邻域,内点,外点,边界点,聚点,开集,闭集,连通集,区域,闭区域,有界集,无界集。2、 多元函数:,图形:3、 极限:4、 持续:5、 偏导数:6、 方向导数: 其中为得方向角。7、 梯度:,则。8、 全微分:设,则(二)性质1、 函数可微,偏导持续,偏导存在,函数持续等概念之间得关系:2、 闭区域上持续函数得性质(有界性定理,最大最小值定理,介值定理)3、 微分法1) 定义: 2) 复合函数求导:链式法则 若,则 ,3) 隐函数求导:两边求偏导,然后解方程(组)(三)应用1、 极值1) 无条件极值:求函数得极值解方程组 求出所有驻点,对于每一种驻点,令,,,① 若,,函数有极小值,若,,函数有极大值;② 若,函数没有极值;③ 若,不定。2) 条件极值:求函数在条件下得极值令: ——— L a gr a nge 函数偏导数存在函数可微函数持续偏导数持续充足条件必要条件定义12234解方程...