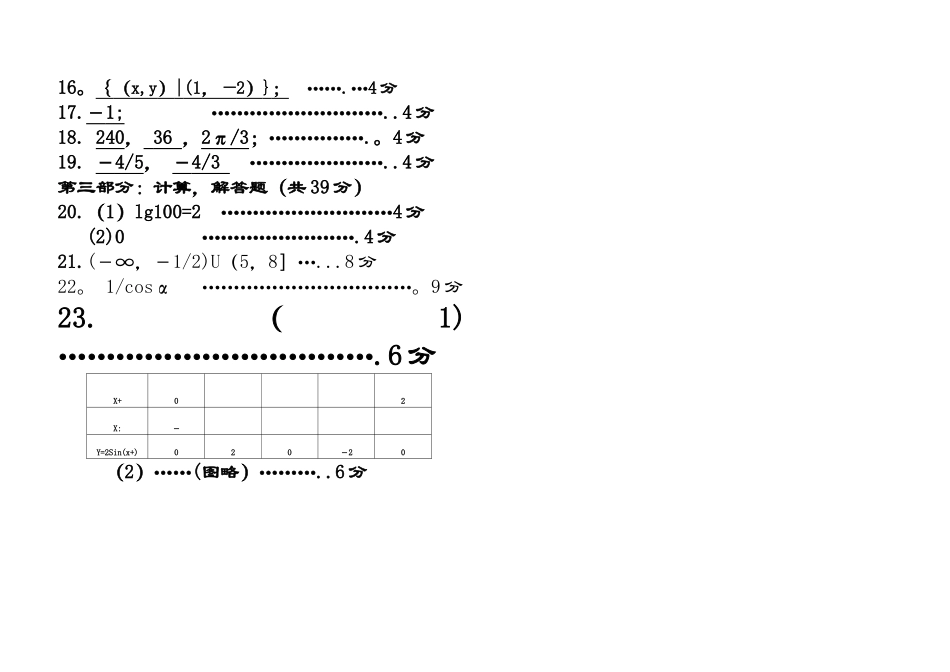
2024-2024 学年度 第一学期数学(基础模块)上期末考试 A 卷学号: 姓名: 班级: 成绩: 本试卷共三个部分:第一部分为选择题:3 分 X15=45 分;第二部分为填空题:4 分 X4=16 分;第三部分为计算,解答题:其中第 20 题为计算题,每小题 5 分,计 10 分,第 21 题 8 分,第 22 题 9 分,第 23 题 12 分;共计总分 100 分。考试时间为 100-120 分钟,开考 60 分钟后方可交卷。第一部分:选择题(每小题 3 分,15 小题,共 45 分)1。已知集合 A ={0,3} ,B={0,3,4},C={1,2,3},则( ) A.{0,1,2,3,4} B. C。{0,3} D。{0}2.设集合则( )A。R B. C。 D。3。奇函数 y=f(x)(xR)的图像必经过的点是( )A。 (—a,—f(a) ) B。 (—a,f(a) ) C。 (a,-f(a) ) D. (a, )4.一元二次方程 x2 – mx + 4 = 0 有实数解的条件是 m ∈( )A.(-4,4) B。[-4,4]C。(-∞,-4)∪(4, +∞) D.(-∞,-4]∪[4, +∞)5。已知函数,则 f(—x)=( )A、 B、 -f(x) C、 - D、 f(x)6.函数 f(x)=( )A、 在()内是减函数 B、 在()内是减函数 C、在()内是减函数 D 、 在()内是减函数7。下列不等式中,解集是空集的是( )A. x 2 — 3 x–4 >0 B. x 2 — 3 x + 4≥ 0C. x 2 — 3 x + 4<0 D。 x 2 — 4x + 4≥08.已知,则( )A。 16 B。 8 C. 4 D。 29.已知,则的最大值是( )A。 B。 C。 D。 10。计算( )A. B。 C。 D。 11。若的终边过点()则值为( )A、 B、 C、 D、12。的值为( )A、 B、 C、 D、13.的值为( )A、 B、 C、 D、14。 当时,在同一坐标系中,函数与函数的图象只可能是( )15。设函数 (且),,则( )A. 2 B. C. 3 D. 第二部分:填空题部分(每小题 4 分,共 16 分)16。 若那么 ;17.设 f(x)= 则 f(—2)=_______________;18. = 度 = 度,120= 弧度19。 若是第四象限角,,则 Sin= ,= 第三部分:计算,解答题部分(39 分)20。计算(每小题 5 分,共 10 分)(1)2lg3+lg7+lg—lg+lg1 (2)Sin—Cos+Cos—Sinπ21.求函数 的定义域(8 分) 22.化简(9 分)23.画函数 y=2Sin(x+)在长度为一个周期的闭区间上的图象要求:(共 12 分)(1)先填空:(6 分)X+02X:Y=2Sin(x+)(2)画一周期的图象(...