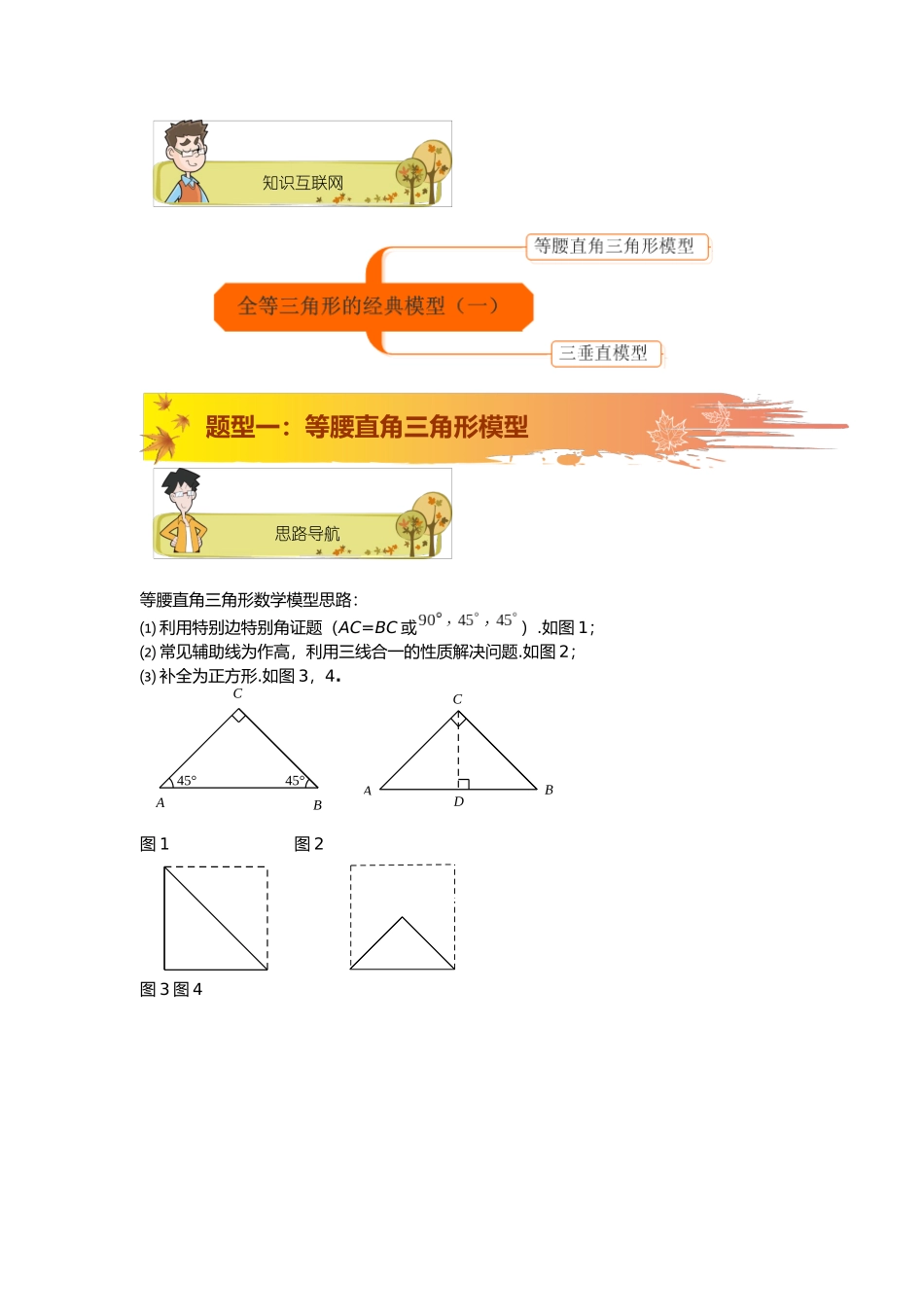
满分晋级三角形 9 级全等三角形的经典模型(二)三角形 8 级全等三角形的经典模型(一)三角形 7 级倍长中线与截长补短秋季班第四讲秋季班第三讲秋季班第二讲漫画释义作弊?3全等三角形的经典模型(一)45°45°CBA知识互联网思路导航等腰直角三角形数学模型思路:⑴ 利用特别边特别角证题(AC=BC 或).如图 1;⑵ 常见辅助线为作高,利用三线合一的性质解决问题.如图 2;⑶ 补全为正方形.如图 3,4.图 1 图 2图 3 图 4 题型一:等腰直角三角形模型DCBA典题精练【例1】 已知:如图所示,Rt△ABC 中,AB=AC,,O 为 BC 的中点,⑴ 写出点 O 到△ABC 的三个顶点 A、B、C 的距离的关系(不要求证明)⑵ 假如点 M、N 分别在线段 AC、AB 上移动,且在移动中保持AN=CM.试推断△OMN 的形状,并证明你的结论.⑶ 假如点 M、N 分别在线段 CA、AB 的延长线上移动,且在移动中保持 AN=CM,试推断⑵中结论是否依旧成立,假如是请给出证明.【解析】⑴OA=OB=OC⑵ 连接 OA, OA=OCAN=CM∴△ANO≌△CMO ∴ON=OM∴∴∴∴△OMN 是等腰直角三角形△⑶ ONM 依旧为等腰直角三角形,证明: ∠BAC=90°,AB=AC,O 为 BC 中点∴∠BAO=∠OAC=∠ABC=∠ACB=45°,∴AO=BO=OC, 在△ANO 和△CMO 中,∴△ANO≌△CMO(SAS)∴ON=OM,∠AON=∠COM,又 ∠COM∠AOM=90°,∴△OMN 为等腰直角三角形.【例2】 两个全等的含,角的三角板和三角板,如图所示放置,三点在一条直线上,连接,取的ABCOMNABCOMNABCOMNMEDCBA中点,连接,.试推断的形状,并说明理由.[解析]是等腰直角三角形.证明:连接.由题意,得∴为等腰直角三角形. ,∴.∴,∴≌.∴.又.∴,∴是等腰直角三角形.【例3】 已知:如图,中,,,是的中点,于,交于,连接.求证:.【解析】证法一:如图,过点作于,交于. ,,∴. ,∴. ,∴ ,∴.∴.在和中,∴.∴.在和中,∴.∴.MEDCBAFEDCBANM12ABCDEF3证法二:如图,作交的延长线于. ,∴, ,∴,∴.在和中,∴.∴, ,∴.在和中,∴.∴∴.【例4】 如图,等腰直角中,,为部一点,满足,求证:.【解析】补全正方形,连接 DP,易证是等边三角形,,,∴,,∴,∴.[探究对象]等腰直角三角形添补成正方形的几种常见题型在解有关等腰直角三角形中的一些问题,若遇到不易解决或解法比较复杂时,可将等腰直角三角形引辅助线转化成正方形,再利用正方形的一些性质来解,常...