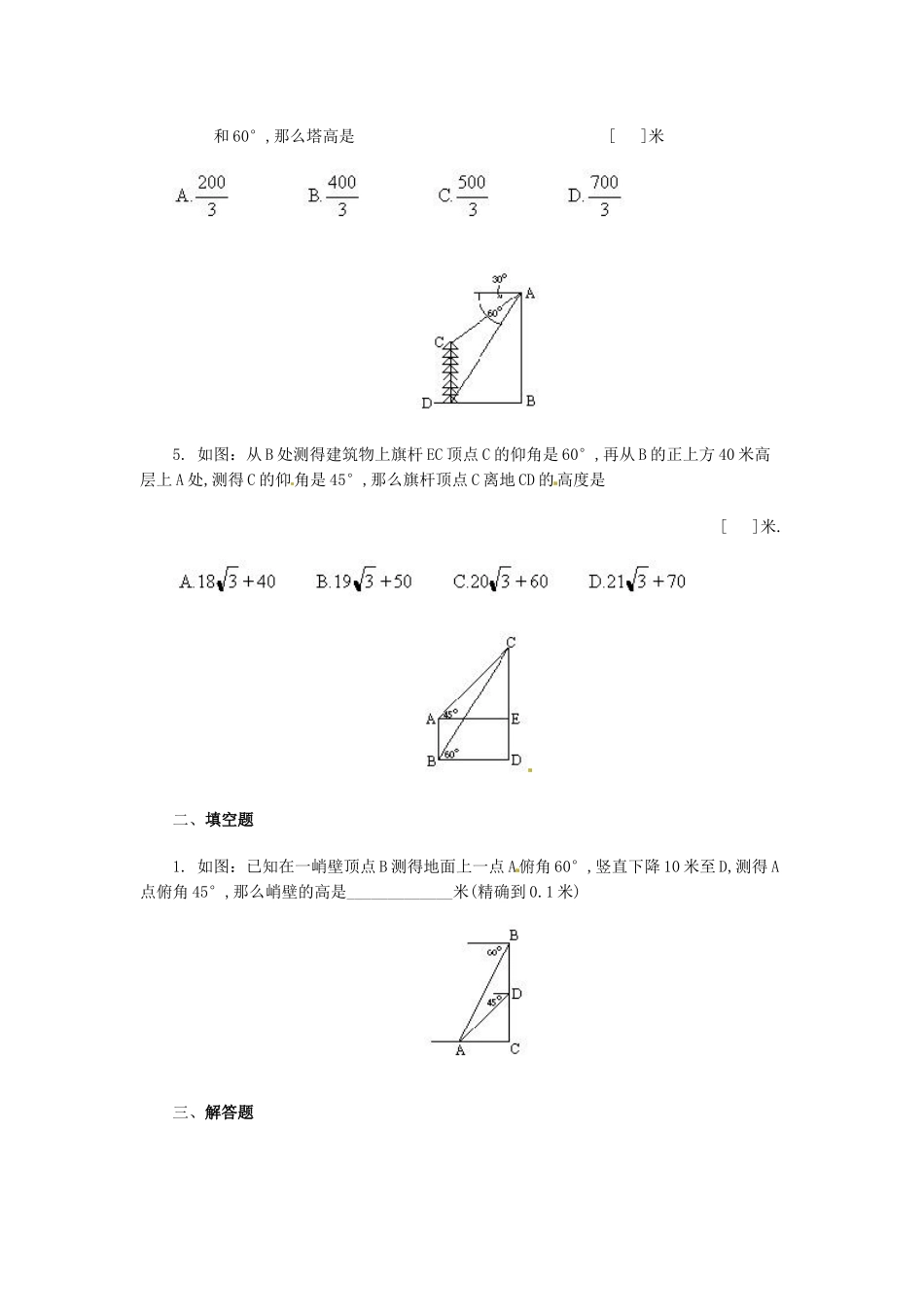
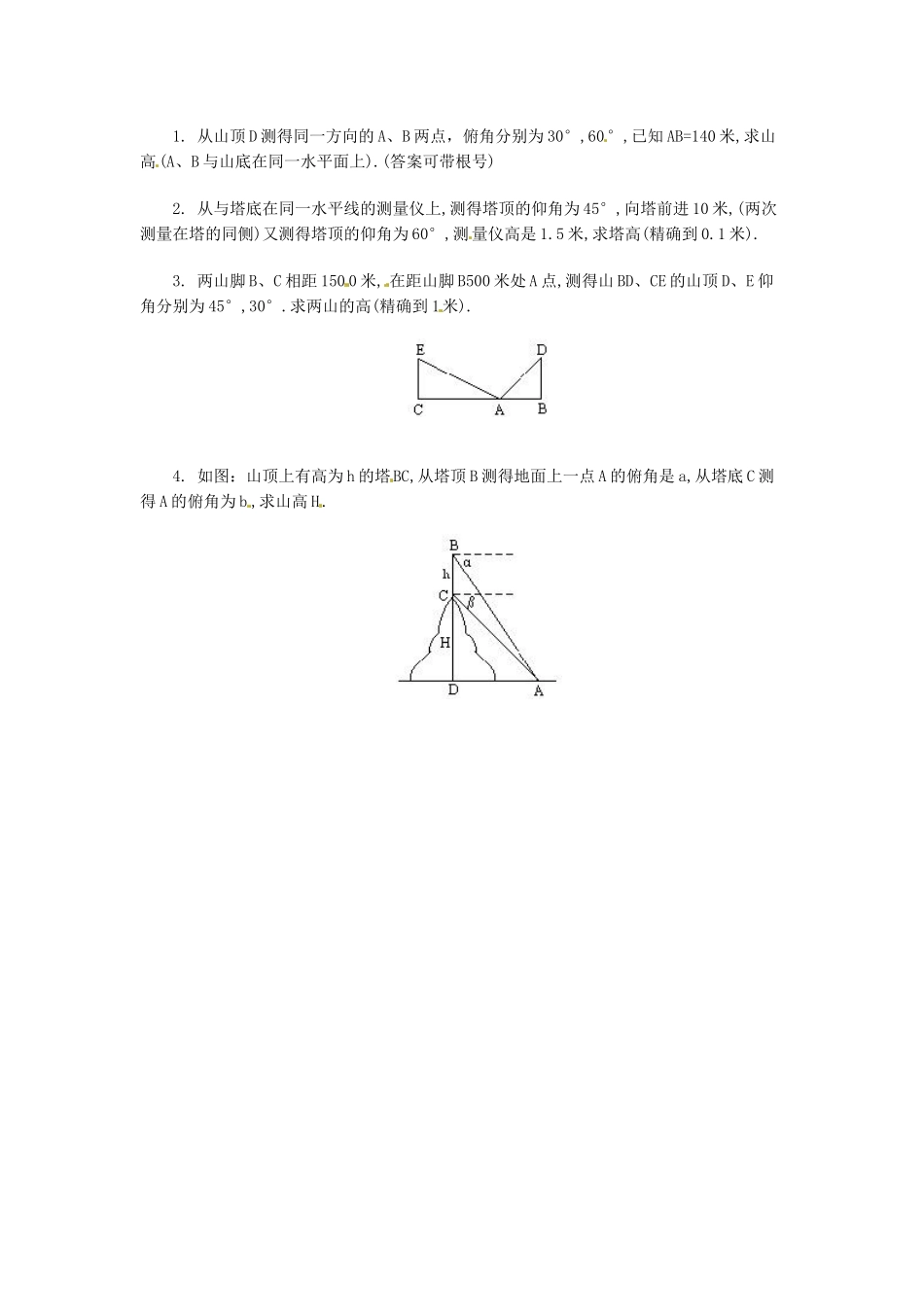
28.2 解直角三角形(2)1. 如图,由 D 点测塔顶 A 点和塔基 B 点仰角分别为 60°和 30°.已知塔基出地平面 20 米(即 BC 为 20 米)塔身 AB 的高为 [ ]2.如图,一敌机从一高炮正上方 2000 米经过,沿水平方向飞行,稍后到达 B 点,这时仰角为 45°,1 分钟后,飞机到达 A 点,仰角 30°,则飞机从 B 到 A 的速度是 [ ]米/分.(精确到米)A.1461 B.1462 C.1463 D.14643. 如图所示,河对岸有水塔CD.今在 A 处测得塔 顶 C 的仰角为 30°,前进 20 米到达 B处,又测得 C 的仰角为 45°,则塔高 CD(精确到 0.1m)是[ ]mA.25.3 B.26.3 C.27.3 D.28.34. 如图:在 200 米高的峭壁上,测得一塔的塔顶与塔基的俯角分别为 30和 60°,那么塔高是 [ ]米5. 如图:从 B 处测得建筑物上旗杆 EC 顶点 C 的仰角是 60°,再从 B 的正上方 40 米高层上 A 处,测得 C 的仰角是 45°,那么旗杆顶点 C 离地 CD 的高度是[ ]米.二、填空题1. 如图:已知在一峭壁顶点 B 测得地面上一点 A俯角 60°,竖直下降 10 米至 D,测得 A点俯角 45°,那么峭壁的高是_____________米(精确到 0.1 米)三、解答题1. 从山顶 D 测得同一方向的 A、B 两点,俯角分别为 30°,60°,已知 AB=140 米,求山高(A、B 与山底在同一水平面上).(答案可带根号)2. 从与塔底在同一水平线的测量仪上,测得塔顶的仰角为 45°,向塔前进 10 米,(两次测量在塔的同侧)又测得塔顶的仰角为 60°,测量仪高是 1.5 米,求塔高(精确到 0.1 米).3. 两山脚 B、C 相距 150 0 米, 在距山脚 B500 米处 A 点,测得山 BD、CE 的山顶 D、E 仰角分别为 45°,30°.求两山的高(精确到 1米).4. 如图:山顶上有高为 h 的塔BC,从塔顶 B 测得地面上一点 A 的俯角是 a,从塔底 C 测得 A 的俯角为 b ,求山高 H.参考答案一、选择题1. C 2. D 3. C 4. B 5. C 二、填空题23.7三、解答题1.70√3米2. 25.2 米3. 500 米,577 米.4. 解:∵DA=(h+H)ctga,DA=Hctgb则 Hctgb=hctga+Hctga即 H(ctgb-ctga)=hctga