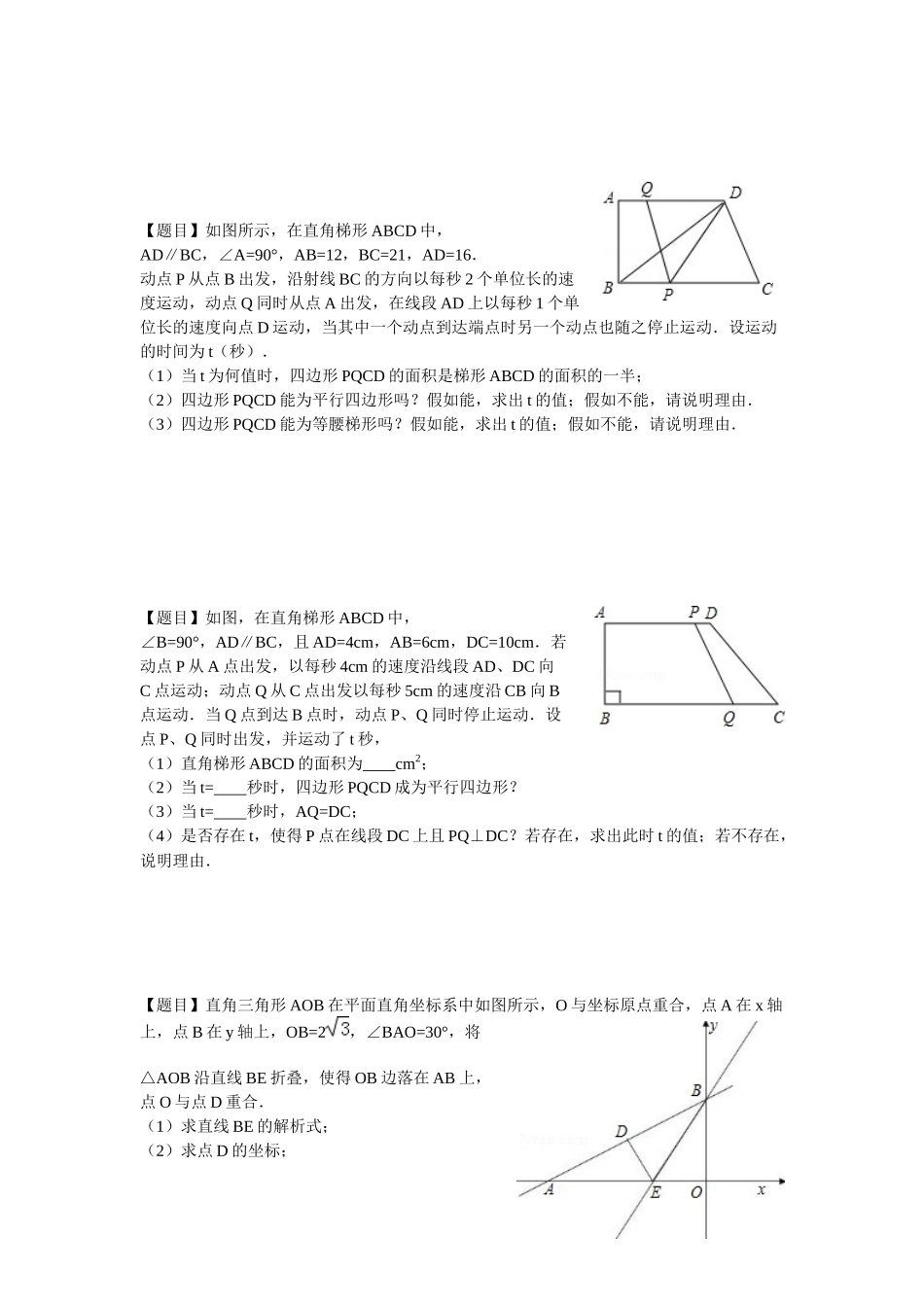
动点产生的平行四边形学生姓名授课日期老师姓名授课时长知识定位学习内容: 平行四边形的性质和判定;动点产生的平行四边形学习目标:1.理解平行四边形的性质和判定; 2.能应用平行四边形的性质和判定进行相关计算和证明; 3.培育学生能在点的运动过程中寻找平行四边形,继而解决相关问题; 4.培育学生分类讨论的能力,能应用分类讨论思想解决相关问题; 5.体验运动过程,培育学生动态数学思维能力。知识梳理知识梳理 1. 动点产生的平行四边形一.平行四边形的性质:中心对称图形对角线互相平分对角相等对边平行且相等平行四边形 的性质二.平行四边形的判定:3.对角线:对角线互相平分的四边形2.边:①两组对边分别平行的四边形; ②两组对边分别相等的四边形; ③一组对边平行且相等的四边形。1.角:对角相等的四边形平行四边形的判定 三、动点形成的平行四边形问题的解题方法和策略: 1.分清楚每个点的位置和运动情况; 2.找到四个顶点中不动点和不变的线段; 3.根据不变的线段分边和对角线两大类计算; 4.在计算过程中注意平行四边形的对称性; 5.准确画图是计算的关键。例题精讲【题目】在直角坐标平面内,为原点,、D (10 ,0)。联结DC ,且直线DC 与y 轴交于点E 。( 2 ) 如 点 M 是 直 线 DC 上 的 一 个 动 点 , 在 x 轴 上 方 的 平 面 内 有 另 一 点 N , 且 以O、E、M、N 为顶点的四边形是菱形,请求出点 N 的坐标。【题目】如图,在平面直角坐标系中,点O 是坐标原点,正比例函数 y=kx (x 为自变量)的图像与双曲线y=− 2x 交于点 A ,且点 A 的横坐标为−√2。(1)求k 的值;(2)将直线 y=kx (x 为自变量)向上平移 4 个单位得到直线BC ,直线BC 分别交x 轴、 y 轴于B 、C ,如点D 在直线BC 上,在平面直角坐标系中求一点P ,使以O 、B 、D 、P 为顶点的四边形是菱形。【题目】如图所示,在直角梯形 ABCD 中,AD∥BC,∠A=90°,AB=12,BC=21,AD=16.动点 P 从点 B 出发,沿射线 BC 的方向以每秒 2 个单位长的速度运动,动点 Q 同时从点 A 出发,在线段 AD 上以每秒 1 个单位长的速度向点 D 运动,当其中一个动点到达端点时另一个动点也随之停止运动.设运动的时间为 t(秒).(1)当 t 为何值时,四边形 PQCD 的面积是梯形 ABCD 的面积的一半;(2)四边形 PQCD 能为平行四边形吗?假如能,求出...