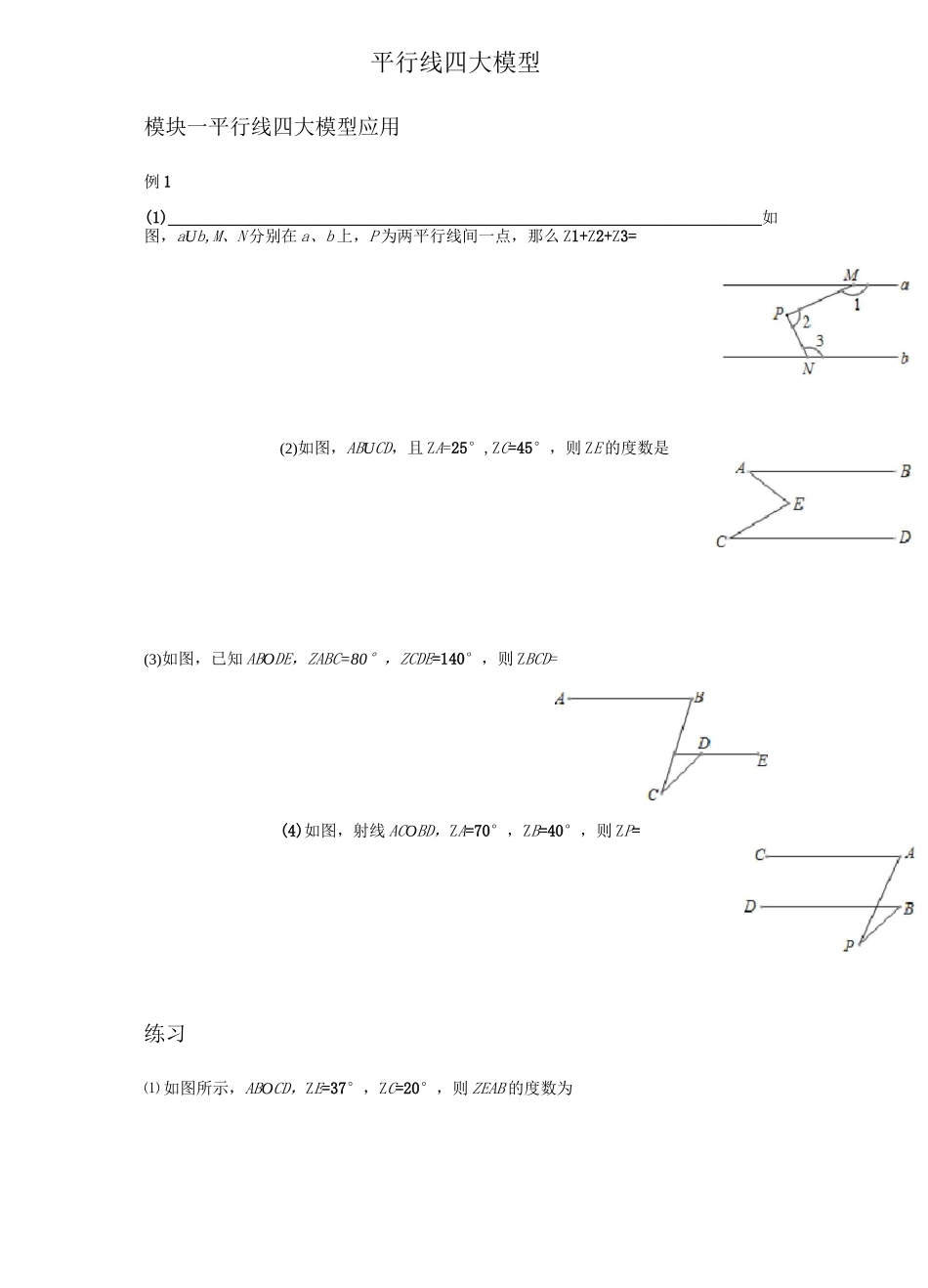
平行线四大模型模块一平行线四大模型应用例 1(1)_________________________________________________________________________如图,aUb,M、N 分别在 a、b 上,P 为两平行线间一点,那么 Z1+Z2+Z3=(2)如图,ABUCD,且 ZA=25°,ZC=45°,则 ZE 的度数是(3)如图,已知 ABODE,ZABC=80°,ZCDE=140°,则 ZBCD=(4)如图,射线 ACOBD,ZA=70°,ZB=40°,则 ZP=练习⑴ 如图所示,ABOCD,ZE=37°,ZC=20°,则 ZEAB 的度数为(2)如图,ABUCD,ZB=30°,ZO=ZC.则 ZC=例 2如图,已知 ABDDE,BF、DF 分别平分/ABC、/CDE,求 ZC、ZF 的关系.练习如图,已知 ABODE,ZFBC=1ZABF,ZFDC=1ZFDE.nn⑴ 若〃=2,直接写出 ZC、ZF 的关系;⑵ 若 n=3,试探究 ZC、ZF 的关系;⑶ 直接写出 ZC、ZF 的关系(用含 n 的等式表示).如练如己知 ABDDE,BF、DF 分别平分/ABC、/CDE,求/C、/F 的关系.如/3==/1+/2,求证:/A+/B+/C+/D=180°.已知 ABDCD,BE 平分/ABC,DE 平分/ADC.求证:2/E=/A+/C.练习如图,AB 丄 BC,AE 平分/BAD 交 BC 于 E,AE 丄 DE,/1+/2=90°,M、N 分别是 BA、CD 的延长线上的点,/EAM 和/EDN 的平分线相交于点 F,则 ZF 的度数为()A.120°B.135°C.145°D.150模块二平行线四大模型构造例5如图,直线 AB//CD,/EFA=30°,/FGH=90°,/HMN=30°,/CNP=50°,则/GHM=.AB练习如图,直线 ABDCD,ZEFG=100°,/FGH=140°,则/AEF+/CHG=例6已知/B=25°,/BCD=45°,/CDE=30°,/E=10°,求证:ABUEF.练习1、已知 ABUEF,求/1-/2+/3+/4 的度数.AAAB'屯A2、(1)如图(1),已知 MA^NAn,探索 ZA]、ZA2、…、/A”,ZB「AB-ABn1之间的关系.(2) 如图(2),己知 MA1DNA4,探索 ZA]、ZA2、ZA3、ZA4,"、ZB2之间的关系.(3) 如图(3),已知叽口叫探索 ZA.ZA?、…、ZA”之间的关系.3、如图所示,两直线 ABDCD 平行,求 Z1+Z2+Z3+Z4+Z5+Z6.挑战压轴题如图 1,直线 ABDCD,P 是截线 MN 上的一点,MN 与 CD、AB 分别交于 E、F.(1)若 ZEFB=55°,ZEDP=30°,求 ZMPD 的度数;⑵ 当点 P 在线段 EF 上运动时,ZCPD 与/ABp的平分线交于 Q,问:磊是否为定值?若是定值,请求出定值;若不是,说明其范围;⑶ 当点 P 在线段 EF 的延长线上运动时,/CDp与/ABp的平分线交于 Q,问磊的值足否定值,请在图 2 中将图形补充完整并说明理由.