椭圆的标准方程教课件

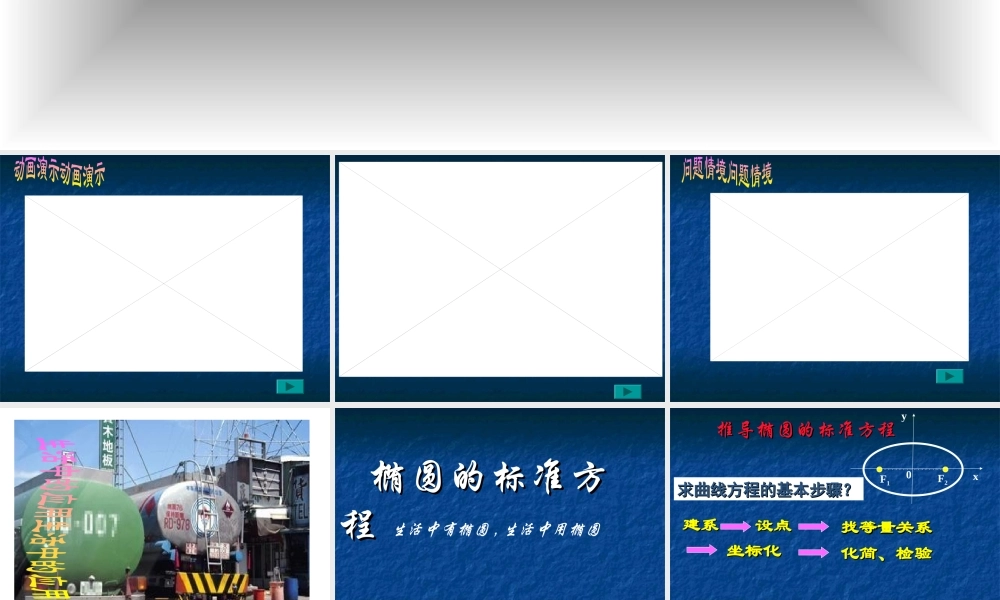
椭圆的标准方椭圆的标准方程程 生活中有椭圆 , 生活中用椭圆求曲线方程的基本步骤？求曲线方程的基本步骤？设点设点建系建系找等量关系找等量关系坐标化坐标化化简、检验化简、检验推导椭圆的标准方程推导椭圆的标准方程F1F2xy0[1] 建系 : 以过焦点 F1 ， F2 的直线为 x 轴，线段 的 垂直平分线为 y 轴，建立直角坐标系，则[2] 设点 : 设 M(x,y) 为椭圆上的任意一点[3] 找关系 : M 与 F1,F2 距离 之和 等于 2a (2a>2c), 所以有 MF1+ MF2=2a[4] 代坐标 :F1F2M0xyaycxycx2)()(2222)0,(),0,(21cFcF [5] 化简 :21FF2222)(2)(ycxaycx∴∴)()(22222222caayaxca∴∴2222222222422yacacxaxaxccxaa222)(ycxacxa∴∴令令,222bca0b 0 ca022ca222222bayaxb∴∴则，椭圆的方程为：则，椭圆的方程为：12222 byax求曲线方程的基本步骤？求曲线方程的基本步骤？设点设点建系建系找等量关系找等量关系坐标化坐标化化简、检验化简、检验推导椭圆的标准方程推导椭圆的标准方程F1F2xy0xy0F1F2椭圆的标准方程xOyF1F2MFF11(0 ,-c)(0 ,-c) 、、 FF22(0, c)(0, c)xOyF1F2MFF11(-c,0)(-c,0) 、、 FF22(c,(c,0)0))0(12222babyax)0(12222babxay)0,0(222cabacab1162522 yx1 、填空：(1) 已知椭圆的方程为 ，则a=___ ， b=___ ， c=____ ，焦点坐标为____________543(3,0) 、 (-3,0)(2) 已知椭圆的方程为 ，则 a=_____ ， b=_______ ， c=_______ ，焦点坐标为 ___________14522 xy521(0,-1) 、 (0,1)22 、、说出适合下列条件的椭圆标准方程说出适合下列条件的椭圆标准方程（（ 11 ） ，焦点在） ，焦点在 x x 轴上；轴上； （（ 22 ） ，焦点在） ，焦点在y y 轴上。轴上。1162522 yx11622 xy15,1 cb3,5ca例例 11 、将圆 上的点的横坐标保、将圆 上的点的横坐标保持不变，纵坐标变为原来的一半，求所得持不变，纵坐标变为原来的一半，求所得的曲线的方程，并说明它是什么曲线。的曲线的方程，并说明它是什么曲线。422 yx解 : 设所得曲线上任一点坐标为 P(x,y), 圆上的对应点的坐标 P’(x’,y’),由题意可得：yyxx2''因为42'2' yx所以4422yx即1422 yx这就是变换后所得曲线的方程，它表示一个椭圆。...