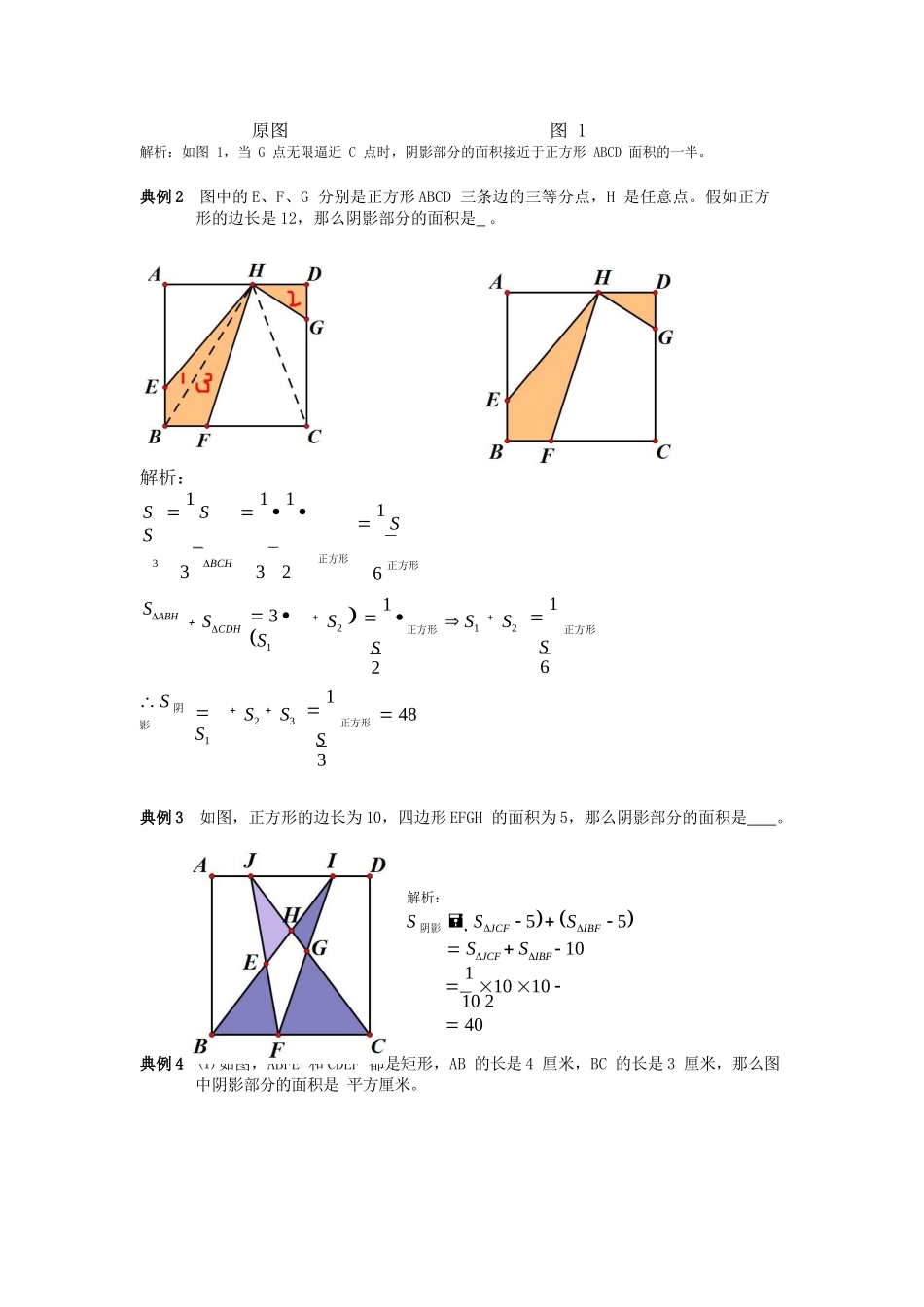
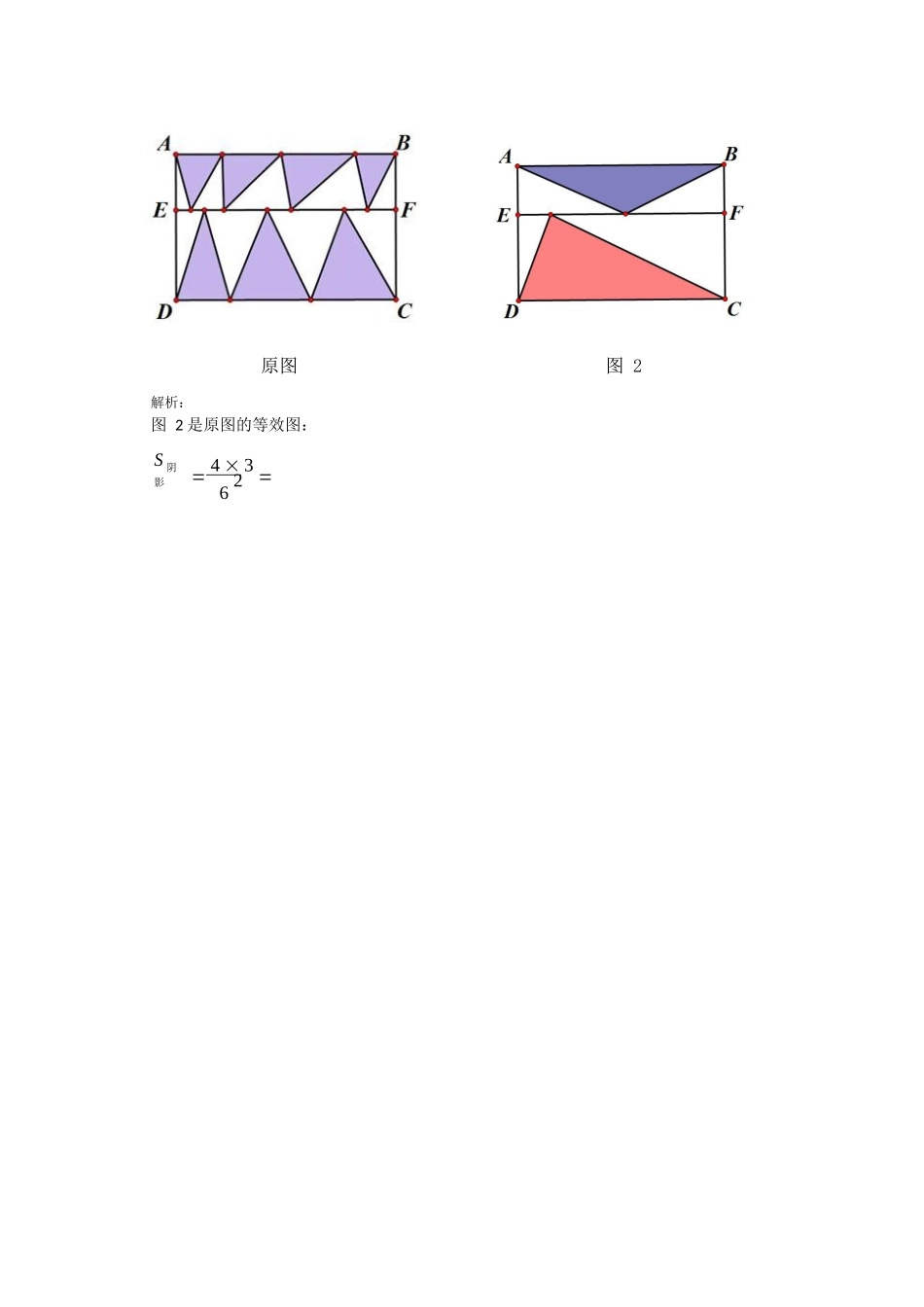
第 1 讲. 共边模型等积模型共边模型一半模型燕尾模型典例 1 正方形 ABCD 和正方形 CEFG,且正方形 ABCD 边长为 10 厘米,则图中阴影面积为多少平方厘米?原图图 1解析:如图 1,当 G 点无限逼近 C 点时,阴影部分的面积接近于正方形 ABCD 面积的一半。典例 2 图中的 E、F、G 分别是正方形 ABCD 三条边的三等分点,H 是任意点。假如正方形的边长是 12,那么阴影部分的面积是 。解析:S 1 S 1 1 S 1 S33 BCH32正方形6 正方形SABH SCDH 3 S1 S2 1 S2正方形 S1 S2 1 S6正方形 S 阴影 S1 S2 S3 1 S3正方形 48典例 3 如图,正方形的边长为 10,四边形 EFGH 的面积为 5,那么阴影部分的面积是 。解析:S 阴影 SJCF 5 SIBF 5 SJCF SIBF 10 1 10 10 10 2 40典例 4 ⑴ 如图,ABFE 和 CDEF 都是矩形,AB 的长是 4 厘米,BC 的长是 3 厘米,那么图中阴影部分的面积是 平方厘米。原图图 2解析:图 2 是原图的等效图:S 阴影 4 3 6 2⑵ 一个长方形分成 4 个不同的三角形,绿色三角形面积占长方形面积的 15%,黄色三角形面积是 21cm2。问:长方形的面积是多少平方厘米?解析:根据一半模型得:黄色与绿色面积和占整个长方形面积的一半。S 长方形 2150% 15% 60cm2典例 5 如图,正方形 ABCD 的边长为 6,AE=1.5,CF=2。长方形 EFGH 的面积为 。解析:根据一半模型得,长方形 EFGH 的面积为 ΔDEF 面积的 2 倍.S 阴影 S 正方形 SADE SBEF SCDF 36 1 6 3 1 4 9 1 2 6 16.522222S2x 3y 30典例 6 如图,已知 BD=DC,EC=2AE,三角形 ABC 的面积是 30,求阴影部分面积。解析: 设 SCDF x, SCEF y,则SBDF x, SAEF 1 y2 BCE 2x y 2 30 2033SACD x 2 y 1 30 152 2x y 20 x 7.5 S x y 12.5 y 5阴影