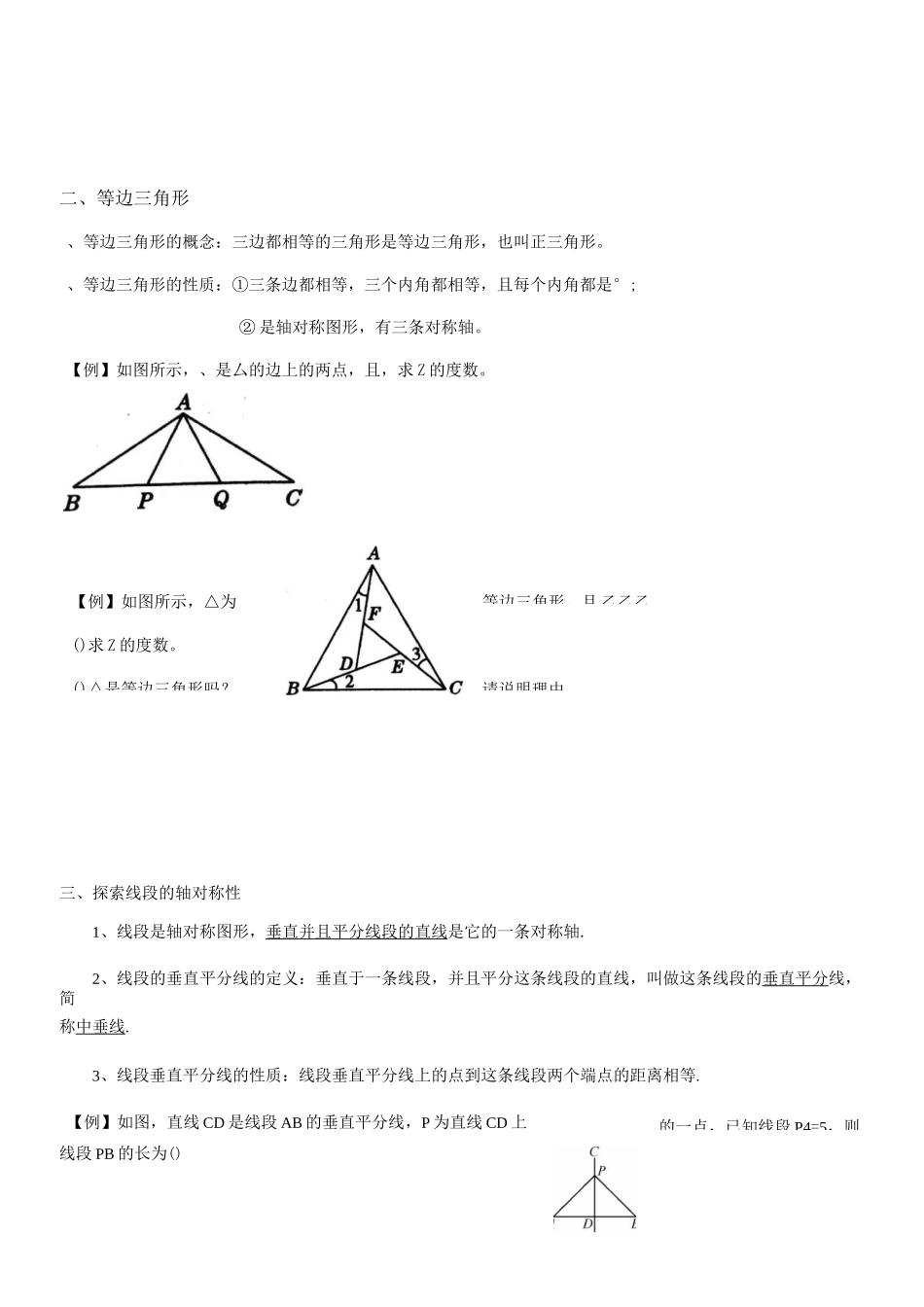
【】如图所示,是厶的角平分线,Z 个。分别是。(三)简单的轴对称图形、等腰三角形、等腰三角形概念:有两边相等的三角形叫做等腰三角形。相等的两边叫做三角形的腰,第三边叫做底边。腰与底边的夹角叫做底角。两腰的夹角叫做顶角。2、等腰三角形的性质:等腰三角形是轴对称图形;等腰三角形顶角的平分线、底边上的中线、底边上的高重合也称“三线合一”,它们所在的直线都是等腰三角形的对称轴;等腰三角形的两个底角相等【例】如图,在 AABC 中,AB=AC,点 D 在 AC 上,且 BD=BC=AD,求△ABC 中各内角的度数.A、等腰三角形的判别方法:()根据等腰三角形的定义:有两边相等的三角形叫做等腰三角形。()如果一个三角形有两个角相等,那么他们所对的边也相等,简称“等角对等边”。,Z°,则图中的等腰三的一点,已知线段 P4=5,则二、等边三角形、等边三角形的概念:三边都相等的三角形是等边三角形,也叫正三角形。、等边三角形的性质:①三条边都相等,三个内角都相等,且每个内角都是°;② 是轴对称图形,有三条对称轴。【例】如图所示,、是厶的边上的两点,且,求 Z 的度数。三、探索线段的轴对称性1、线段是轴对称图形,垂直并且平分线段的直线是它的一条对称轴.2、线段的垂直平分线的定义:垂直于一条线段,并且平分这条线段的直线,叫做这条线段的垂直平分线,简称中垂线.3、线段垂直平分线的性质:线段垂直平分线上的点到这条线段两个端点的距离相等.【例】如图,直线 CD 是线段 AB 的垂直平分线,P 为直线 CD 上线段 PB 的长为()【例】如图所示,△为()求 Z 的度数。()△是等边三角形吗?等边三角形,且乙乙乙请说明理由。A.6B.5C.4D.3四、探索角的轴对称性.角是轴对称图形,角平分线所在的直线是它的对称轴.【例】如图,已知 BG 是 ZABC 的平分线,DE 丄 AB 于点 E,DF 丄 BC 于点 F,则 DF 的长为()A.2B.3C.4D.6【例 2】如图,AD 是 A4BC 中 ZBAC 的平分线,DE 丄 AB 于点 E,AC=7,DE=4,则 A4DC 的面积等于A.20°B.50°或 80°C.10°D.20°或 80°★对应练习(三)简单的轴对称图形知识点一、等腰三角形1、已知等腰三角形的一个角为 80°,则其顶角为()ADE=6,A.6B.5BD=CE。试说明:4、如图,在△ABC 中,AB=AC,AD 是 BC 边上的中线,BE 丄 AE 于点 E,证明:ZCBE=ZBAD5、如图,在 AABC中,AB=AC,ZA=30°,E 为 BC 延长线一点,ZABC 与 ZACE 的平AAD于点 D,则 ZD...