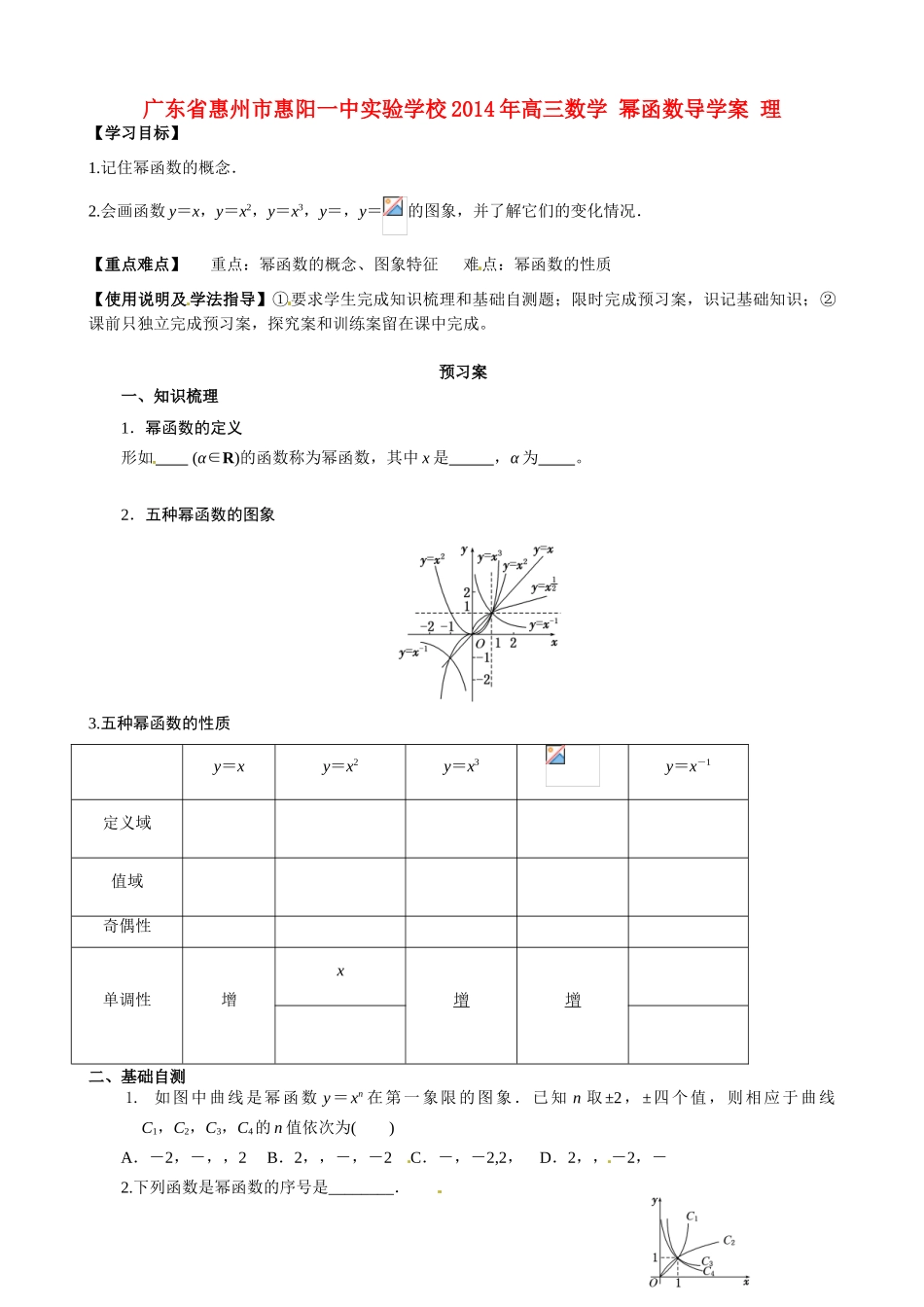
广东省惠州市惠阳一中实验学校 2014 年高三数学 幂函数导学案 理【学习目标】1.记住幂函数的概念.2.会画函数 y=x,y=x2,y=x3,y=,y=的图象,并了解它们的变化情况.【重点难点】 重点:幂函数的概念、图象特征 难点:幂函数的性质【使用说明及 学法指导】①要求学生完成知识梳理和基础自测题;限时完成预习案,识记基础知识;②课前只独立完成预习案,探究案和训练案留在课中完成。预习案一、知识梳理1.幂函数的定义形如 (α∈R)的函数称为幂函数,其中 x 是 ,α 为 。2.五种幂函数的图象3.五种幂函数的性质y=xy=x2y=x3y=x-1定义域值域奇偶性单调性增x 增增二、基础自测1. 如图中曲线是幂函数 y=xn 在第一象限的图象.已知 n 取±2,±四个值,则相应于曲线C1,C2,C3,C4的 n 值依次为( )A.-2,-,,2 B.2,,-,-2 C.-,-2,2, D.2,,-2,-2.下列函数是幂函数的序号是________. ①y=2x;② y=2x-1;③ y=(x+2)2;④ y=;⑤ y=.探究案一、合作探究例 1. 已知幂函数的图象关于 y 轴对称,且在上是减函数,求满足的实数 a 的取值范围。例 2.已知幂函数 f(x)的图象经过点,P(x1,y1),Q(x2,y2)(x1x2f(x2);② x1f(x1);④<.其中正确结论的序号是( )A.①② B.①③ C.②④ D.②③例 3.解关于 x 的不等式: 二、总结整理训练案一、课中训练与检测已知幂函数 f(x)= (m∈N*)(1)试确定该函数的定义域,并指明该函数在其定义域上的单调性;(2)若该函数还经过点(2,),试确定 m 的值,并求满足条件 f(2-a)>f(a-1)的实数 a 的取值范围.二、课后巩固促提升已知函数 f(x)=x2+mx+n 的图象过点(1,3),且 f(-1+x)=f(-1-x)对任意实数都成立,函数 y=g(x)与 y=f(x)的图象关于原点对称.(1)求 f(x)与 g(x)的解析式;(2)若 F(x)=g(x)-λf(x)在(-1,1]上是增函数,求实数 λ 的取值范围.