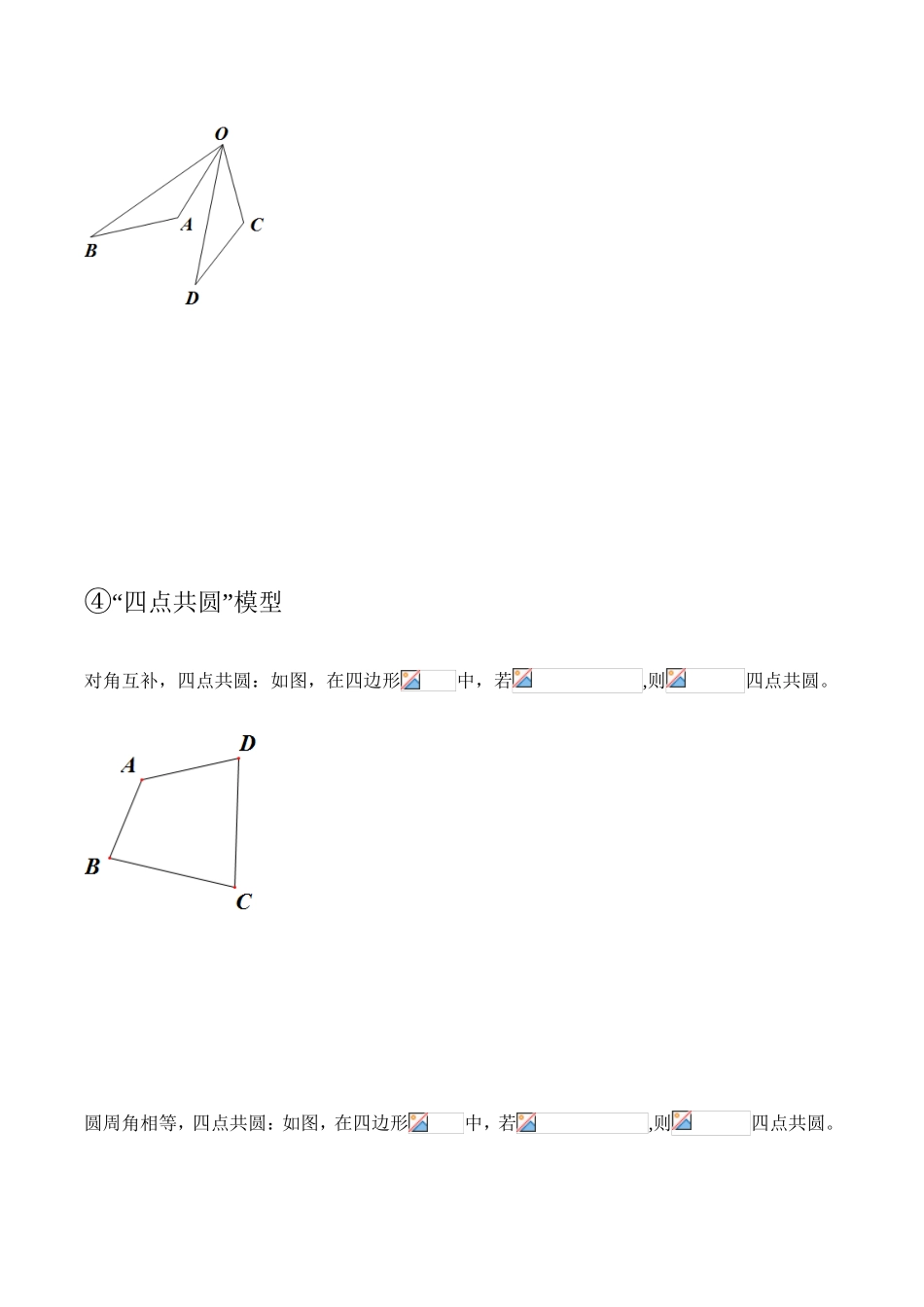
第0章四个基本模型“①爪子图”模型如图,由“②一线三等角”模型如图,若B,C,D三点共线,且,则当且仅当C为BD的中点或AE=BD时,“③旋转角”模型如图,如果绕点旋转角到,则所在直线的夹角也是④“四点共圆”模型对角互补,四点共圆:如图,在四边形中,若,则四点共圆。圆周角相等,四点共圆:如图,在四边形中,若,则四点共圆。第1章一线三等角【1】(2016昌平二模)在等边△ABC中,AB=2,点E是BC边上一点,∠DEF=60°,且∠DEF的两边分别与△ABC的边AB,AC交于点P,Q(点P不与点A,B重合).(1)若点E为BC中点.①当点Q与点A重合,请在图1中补全图形;②在图2中,将∠DEF绕着点E旋转,设BP的长为x,CQ的长为y,求y与x的函数关系式,并写出自变量x的取值范围;(2)如图3,当点P为AB的中点时,点M,N分别为BC,AC的中点,在EF上截取=EP,连接.请你判断线段与ME的数量关系,并说明理由.NMP'DFQEABC图3图1PECBAABEC图2DPQF【2】(2016海淀九上期末)(1)如图1,△ABC中,,AB的垂直平分线交AC于点D,连接BD.若AC=2,BC=1,则△BCD的周长为;(2)O为正方形ABCD的中心,E为CD边上一点,F为AD边上一点,且△EDF的周长等于AD的长.①在图2中求作△EDF(要求:尺规作图,不写作法,保留作图痕迹);②在图3中补全图形,求的度数;③若,则的值为.第2章半角模型【1】(2014平谷一摸)(1)如图1,点E、F分别是正方形ABCD的边BC、CD上的点,∠EAF=45°,连接EF,则EF、BE、FD之间的数量关系是:EF=BE+FD.连结BD,交AE、AF于点M、N,且MN、BM、DN满足,请证明这个等量关系;(2)在△ABC中,AB=AC,点D、E分别为BC边上的两点.①如图2,当∠BAC=60°,∠DAE=30°时,BD、DE、EC应满足的等量关系是__________________;②如图3,当∠BAC=,(0°<<90°),∠DAE=时,BD、DE、EC应满足的等量关系是____________________.【参考:】ABCDEF图1BCDE图2ABCDE图3AMN【2】(2013东城一模)问题1:如图1,在等腰梯形ABCD中,AD∥BC,AB=BC=CD,点M,N分别在AD,CD上,若∠MBN=∠ABC,试探究线段MN,AM,CN有怎样的数量关系?请直接写出你的猜想,不用证明;问题2:如图2,在四边形ABCD中,AB=BC,∠ABC+∠ADC=180°,点M,N分别在DA,CD的延长线上,若∠MBN=∠ABC仍然成立,请你进一步探究线段MN,AM,CN又有怎样的数量关系?写出你的猜想,并给予证明.【3】(2014房山二模)边长为2的正方形ABCD的两顶点A、C分别在正方形EFGH的两边DE、DG上(如图1),现将正方形ABCD绕D点顺时针旋转,当A点第一次落在DF上时停止旋转,旋转过程中,AB边交DF于点M,BC边交DG于点N.(1)求边DA在旋转过程中所扫过的面积;(2)旋转过程中,当MN和AC平行时(如图2),求正方形ABCD旋转的度数;(3)如图3,设MBN的周长为p,在旋转正方形ABCD的过程中,p值是否有变化?请证明你的结论.【4】(2016石景山一模)在正方形ABCD中,E为边CD上一点,连接BE.(1)请你在图1画出△BEM,使得△BEM与△BEC关于直线BE对称;(2)若边AD上存在一点F,使得AF+CE=EF,请你在图2中探究∠ABF与∠CBE的数量关系并证明;(3)在(2)的条件下,若点E为边CD的三等分点,且CE