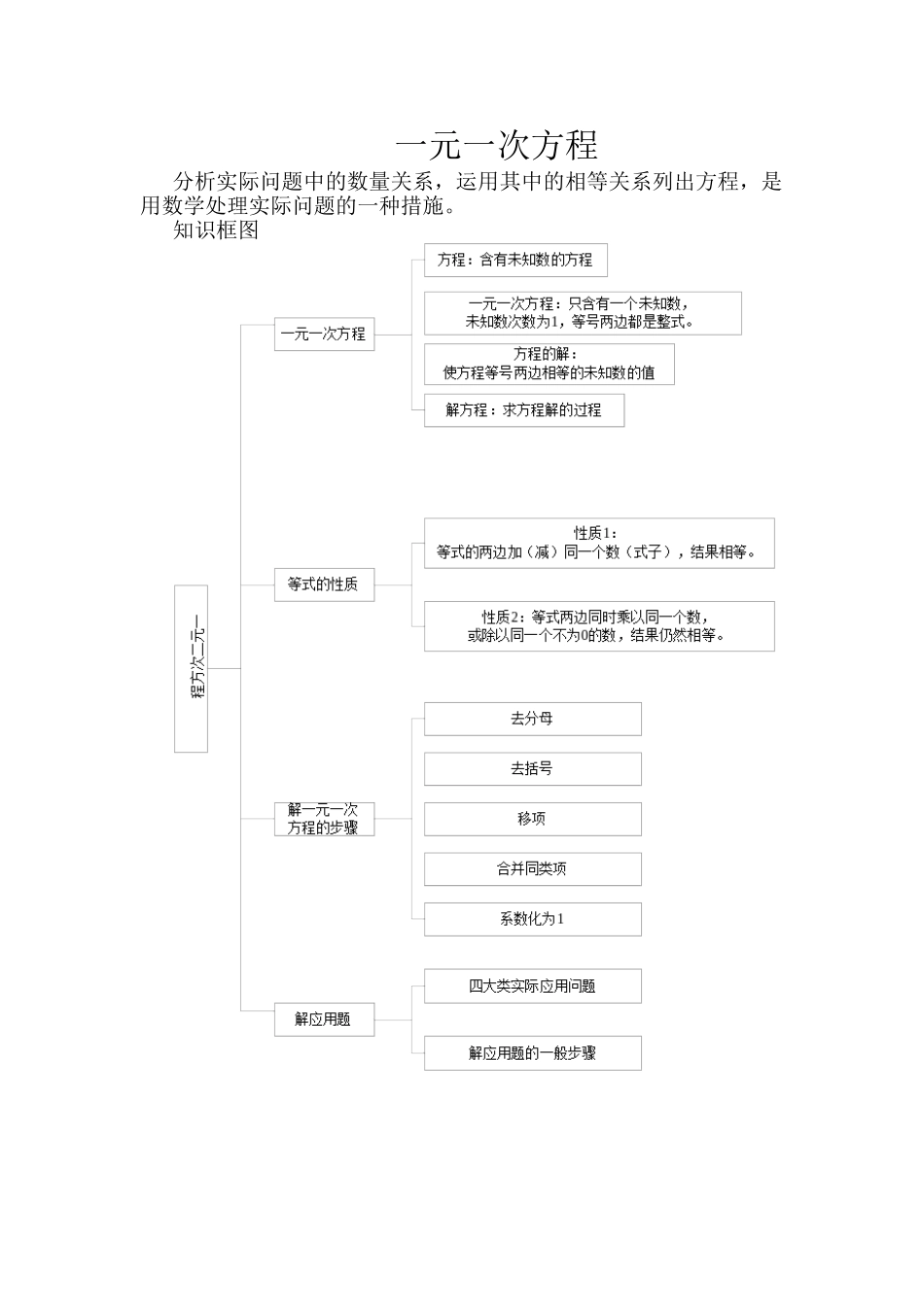
一元一次方程分析实际问题中的数量关系,运用其中的相等关系列出方程,是用数学处理实际问题的一种措施。知识框图(一)方程定义先设字母表达未知数,然后根据相等关系,写出具有未知数的等式叫方程。 (二)一元一次方程1.一元一次方程:方程里只具有一种未知数(元),未知数的次数都是 1,这样的方程叫做一元一次方程。2.解:求出的方程中未知数的值叫做方程的解。(三)等式的性质1.等式两边加(或减)同一种数(或式子),成果仍相等。假如 a= b,那么 a± c= b± c2.等式两边乘同一种数,或除以同一种不为 0 的数,成果仍相等。假如 a= b,那么 a c= b c;假如 a= b,(c‡0),那么 a ∕c = b ∕ c。(四)解方程的环节解一元一次方程的环节:去分母、去括号、移项、合并同类项,未知数系数化为 1。1.去分母:把系数化成整数。2.去括号3.移项:把等式一边的某项变号后移到另一边。4.合并同类项5.系数化为 1(五)一元一次方程的应用1. 实际应用问题的类型(1)列方程处理工程问题注意:工程问题的基本量(工作量、工作效率、工作时间);基本数量关系(总量=效率 X 时间);合作的效率=各单独做的效率之和当工作总量未给出详细数量时,常设工作总量为 1,分析时可采用列表或画图来协助处理题意。(2)列方程处理销售问题注意:销售问题的基本量(商品的售价、商品的利润、商品的利润率),基本量的关系——商品的售价=商品的标价 X 商品销售折扣=商品的进价 X(1+商品的利润率);利润=售价-进价;利润率=%总利润=利润 X 销售量。(3)处理比赛中的积分问题注意:积分多少与胜、平、负的场数有关,并且与比赛积分的规定有关;基本的等量关系——总场数=胜场数+负场数+平场数,总积分=胜场积分+负场积分+平场积分。(4)处理分段计费分问题注意:不一样的阶段用不一样的原则进行计算费用。2. 解应用题的详细环节审、设、列、解、验五个环节。