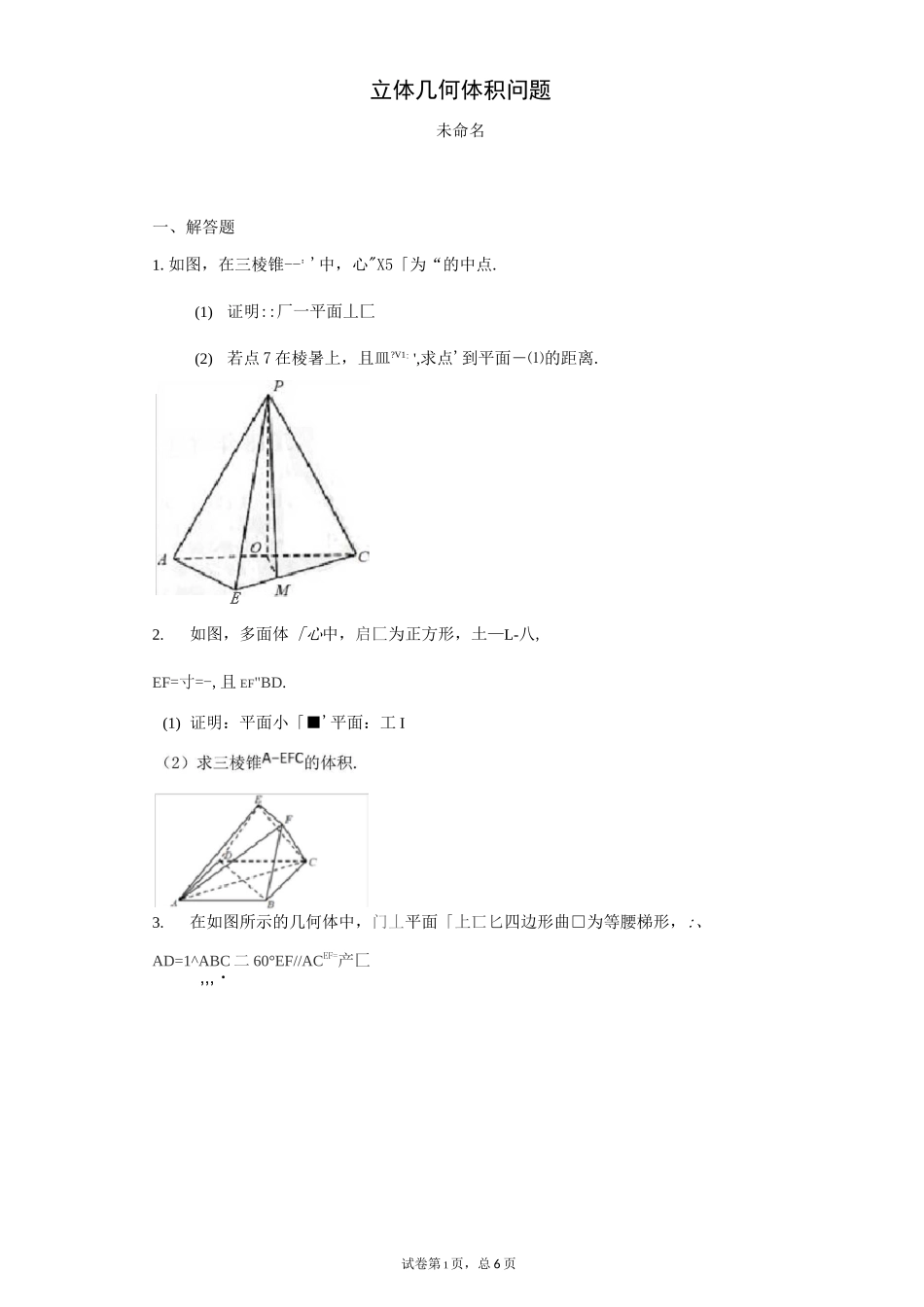
试卷第 1 页,总 6 页立体几何体积问题未命名一、解答题1.如图,在三棱锥--:'中,心"X5「为“的中点.(1)证明::厂一平面丄匚(2)若点 7 在棱暑上,且皿?V1:',求点'到平面―⑴的距离.2.如图,多面体「心中,启匚为正方形,土—L-八,EF=寸=-,且 EF"BD.(1) 证明:平面小「■'平面:工 I3.在如图所示的几何体中,门丄平面「上匸匕四边形曲□为等腰梯形,:、AD=1^ABC 二 60°EF//ACEF=产匚,,,・E试卷第 2 页,总 6 页(2)若多面体皿厂」的体积为,,求线段门的长.4.如图,在四棱锥:中,「,「:,,n 小.,,—、■,点-在线段二 1上,且心AD 丄 AB,卩 A 丄平面 ABCD.(1)证明:平面-f"vl-平面:「;(2)当 f、、时,求四棱锥:m 的表面积.5.如图,在四棱锥 7 匚匚'中,m是等边三角形,皿匚,.U「,二::■:'<仃 I)若平面 F 力平面,心[;“•:,「匚-求三棱锥‘5 的体积「向_丄土丄、ABC-ABC.r—AACCi—AABB—AACCi—6.如图,三棱柱中,平面平面--,平面平面试卷第 3 页,总 6 页“八、’宀-',点、''分别为棱雹、…-的中点,过点的平面交棱于点-使得二'〃平面八 1[\(1)求证:'一平面■J';■I 匸(2)若四棱锥的体积为-,求的正弦值.7.如图,在几何体中,平面'-底面“:,四边形是正方形,BC//BC°口 AR“亠-^.ACBC2BC 艺 ACB 丄丄,°是 1 的中点,且丄 1,(2)若::'」〔〔求几何体 f-的体积.8.在多面体 LT 中,底面书工'是梯形,四边形匚〔佇是正方形,八心 I)「,:卩•I,面 ABCD 丄面 ADEF,AB=AD".8=2.(1)求证:平面 7 匚丄平面玉II(2)设讪为线段 V 上一点,■-切-'-,试问在线段"上是否存在一点 J 使得 V|'■平面匕匸,若存在,试指出点的位置;若不存在,说明理由?试卷第 4 页,总 6 页(3)在(2)的条件下,求点八到平面’「的距离.9.已 知 直 三 棱柱底面 3;:是边长为 2 的等边三角形,"-1 门为棱竺的试卷第 5 页,总 6 页中点,在 1 上,且 T1■.(1)证明:匚匚丄平面 I」;(2)求三棱锥二°:的体积.10.如图,在三棱锥'丄忙中,』—眾,汀一 J 心汽「,^一」■,门为线段5 的中点,将'「心折叠至二二 El,使得 I「丄 I 宀订且小交平面二匕[■于 F.(1)求证:平面二飞丄平面 PAC.(2)求三棱锥‘一匕二的体积.11.在矩形 Z 口所在平面'的同一侧取两点:、:,使匚且=-「,若AB=AF=3AD=4DE=1(1)求证:山)T(2)取匸匚的中点',求证 A:l,:(3) 求...