例题灰色预测VIP免费

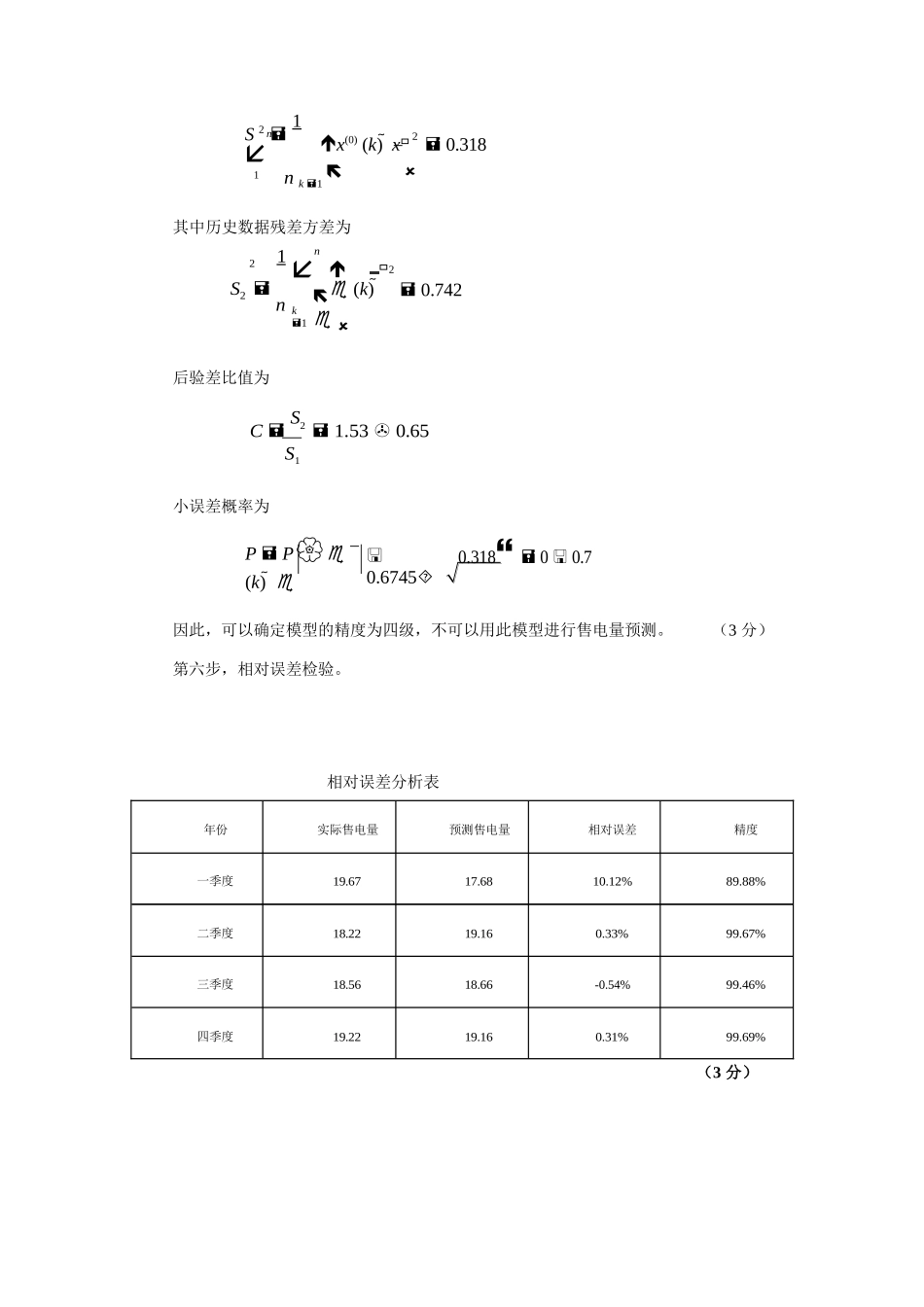
17.39515某开发区2007年四个季度的用电量如下表：季度一季度二季度三季度四季度序号1234实际用电量19.6718.2218.5619.22试用灰色预测模型进行预测，并进行模型精度的后验差检验与预测结果的相对误差检验。解：第一步，计算原始数列x(0)的累加生成值。x(0)x(0)(1),x(0)(2),x(0)(3),x(0)(4)=（19.67,18.22,18.56,19.22）则x(0)的1—AGO为x(1)(1)x(0)(1)19.67x(1)(2)x(1)(1)x(0)(2)37.89x(1)(3)x(1)(2)x(0)(3)56.45x(1)(4)x(1)(3)x(0)(4)75.67（3分）第二步，计算数据矩阵B和数据向量Yn。采用GM（1，1）模型所对应的数据矩阵为1x(1)(1)x(1)(2)1228.781B1x(1)(2)x(1)(3)147.171266.0611x(1)(3)x(1)(4)1218.22Yn18.5619.22第三步，计算GM（1，1）微分方程的参数aˆ和uˆ。将B、Yn代入式可得Aˆ0.02686（3分）（3分）第四步，建立灰色预测模型至此，可求解白化微分方程，首先得到累加数列x(1)的灰色预测模型为xˆ(1)(k1)x(0)(1)uˆeaˆkuˆaˆaˆ（k=0，1，2，…）将有关数据代入后得xˆ(1)(k1)667.2936e0.02686k647.6236再由xˆ(0)(k1)xˆ(1)(k1)xˆ(1)(k)得原始数列的灰色预测模型为xˆ(0)(k1)667.2936(1e0.02686)e0.02686k（k=0，1，2，…）（5分）xˆ(0)(k1)xˆ(1)(k1)xˆ(1)(k)(1eaˆ)(x(0)(1)uˆ)eaˆkaˆ（k=0,1,2,…）由此两模型可得xˆ(0)(k)的模型值xˆ(0)(k)模型值计算表k1234xˆ(0)(k)17.6818.1618.6619.16第五步，模型精度的后验差检验。灰色预测模型建立之后，必须对模型精度进行检验，常用的方法就是后验差检验，经计算得知残差平均值为1nnk1(k)1nnk1x(0)(k)xˆ(0)(k)历史数据方差为S21n2x(0)(k)x0.318nk1其中历史数据残差方差为21nS2nk1(k)0.742后验差比值为CS21.530.65S1小误差概率为PP(k)0.67450.31800.7因此，可以确定模型的精度为四级，不可以用此模型进行售电量预测。（3分）第六步，相对误差检验。相对误差分析表年份实际售电量预测售电量相对误差精度一季度19.6717.6810.12%89.88%二季度18.2219.160.33%99.67%三季度18.5618.66-0.54%99.46%四季度19.2219.160.31%99.69%（3分）12