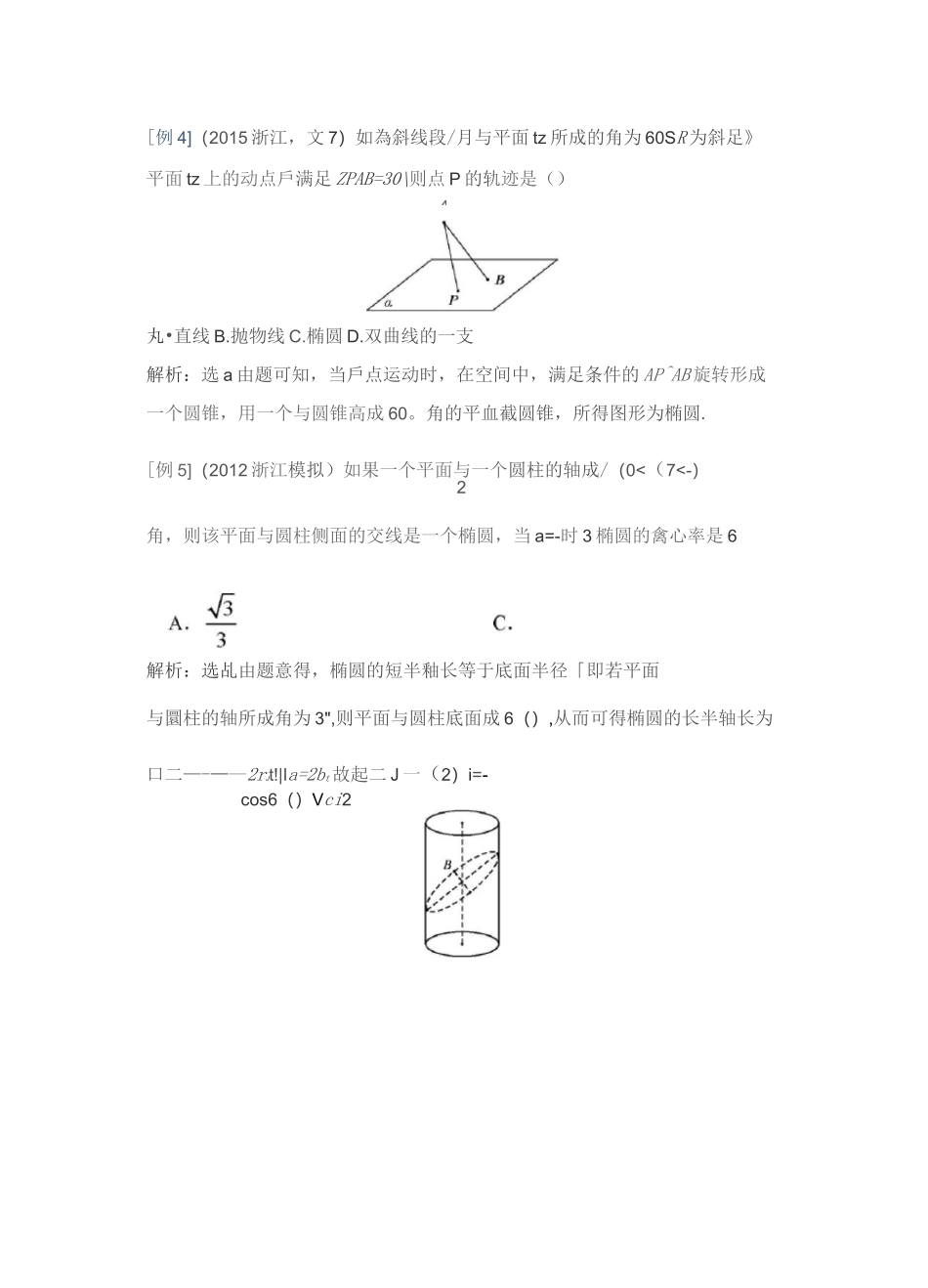
性CA.直线B.圆©考点突破[例 1](2004 北京,理 4)如图,在正方体 ABCD-A^C^中,尸是侧面码 G©内•幼点,若 F 到直线 BC 与直线 qu 的距离相等,则动点 p 的轨迹所在的曲线毘()C.双曲线D.抛物线解析畫选 D.出比;口丄平面 BB{C}C.连接 PC、,则 FG 丄 GD,即点戶到直线 qq 的距离即 PC、,因此,动点戸到定点 q 与定直线 EC 的距离相等,由抛物线的定义可知,动点尸的轨迹为拋物线.立体几何微专题 1:动态问题之轨迹立体几何动态问题的分为以下基本类型:点动问题、线动问题、面动问题、体动问题、多动问题等,很多的动态问题只要知道轨迹,把空间转化为平面问题要解决,立体几何中某些点、线、面依一定的规则运动,构成各式各样的轨迹,探求空间轨迹与求平面轨迹类似,应注意几何条件,善于转化为平面问题.轨迹的几何判断方法:动点 P 满足如下轨迹定义条件时(1)平面内到定点距离等于定长(圆);(2)空间中到定点距离等于定长(球面);(3)两不同平面公共点的集合(直线);(4)平面内到两定点距离之和为定值(大于定点间的距离)(椭圆);(5)平面内到两定点距离之差的绝对值为定值(小于定点间的距离)(双曲线);(6)平面内到定直线距离等于到定点(不在定直线上)距离(抛物线)fA.圆[例 3](2008 浙江,理 10)如图,山〃是平曲&的斜线段,畀为斜足,若点 P 在平面圧内运动,便得 A4 疗戶的面枳为是值,则动点戶的轨迹是B.椭圆G—条直线6 两条卩行直线解析;选乩由题意知’点 P 到线段月〃的即离为定值,则点戶在以 AH旋转轴的圜柱表面上一点,故乎面盘斜截园柱,所得图形为椭圜.[例 2](2(K)6 北京,理斗[平面口的斜线兒 7?交 a 于点厅,过定点兄的线/与川〃垂肓,且交口于点 C,则动点 C 的轨迹足(A.-条直线 B.—个圆 C.-个椭圆 D.双曲线的一支解析:选仏设/与「是其中的两条任恵的直线,则这两条直线确定…个平fib 且斜线川行垂直于这个平面,由过平曲外一点有且只有一个平血与已知直线垂直可知过定点/与虫*垂直所有直线都在这个平面内,故动点「都在这个平面与平面 m 的交线上,故选 A.[例 4](2015 浙江,文 7)如為斜线段/月与平面 tz 所成的角为 60SR 为斜足》平面 tz 上的动点戶满足 ZPAB=30\则点 P 的轨迹是()丸•直线 B.抛物线 C.椭圆 D.双曲线的一支解析:选 a 由题可知,当戶点运动时,在空间中,满足条件的 AP^AB 旋转形成...