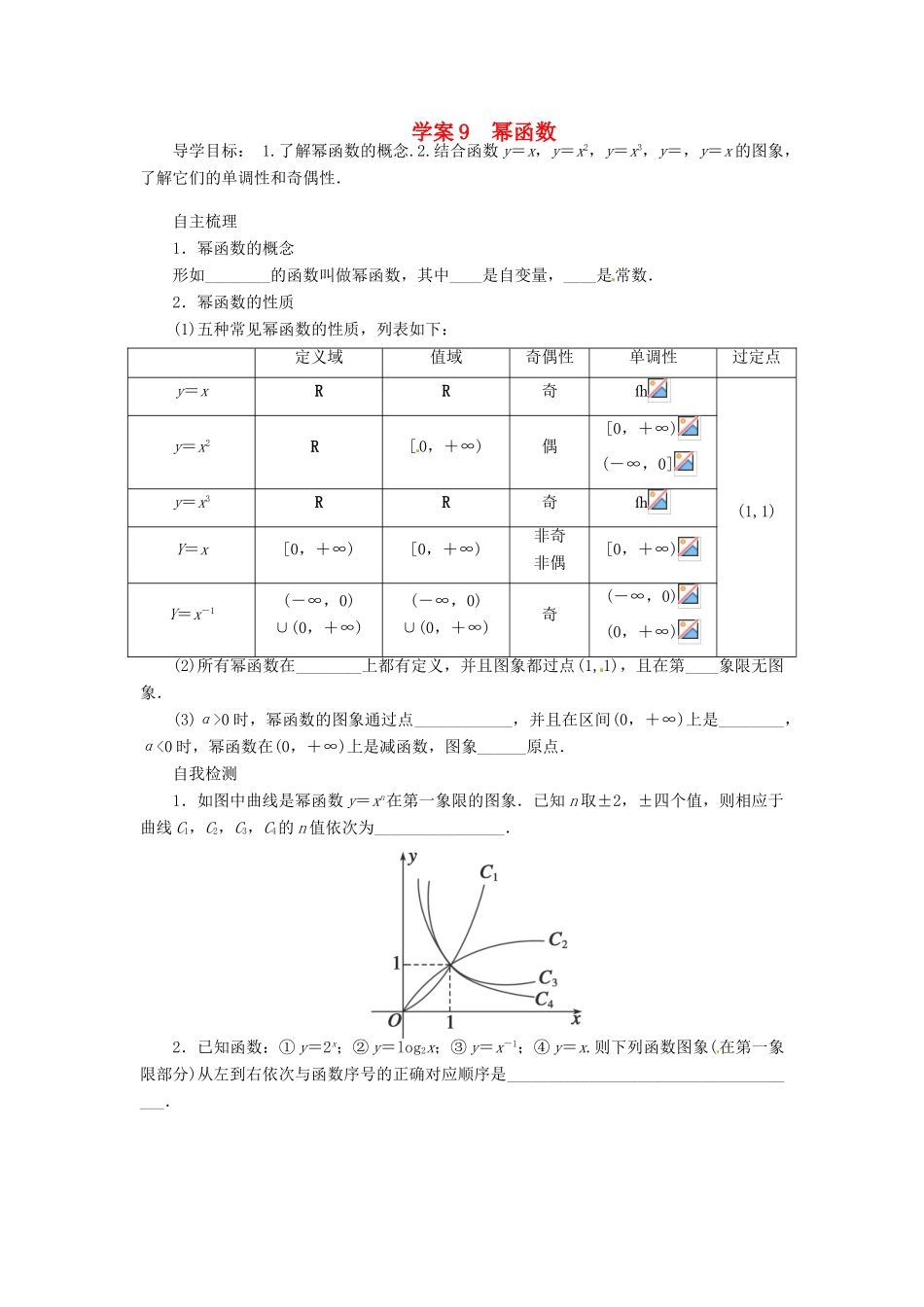
学案 9 幂函数导学目标: 1.了解幂函数的概念.2.结合函数 y=x,y=x2,y=x3,y=,y=x 的图象,了解它们的单调性和奇偶性.自主梳理1.幂函数的概念形如________的函数叫做幂函数,其中____是自变量,____是常数.2.幂函数的性质(1)五种常见幂函数的性质,列表如下:定义域值域奇偶性单调性过定点y=xRR奇(1,1)y=x2R][0,+∞)偶[0,+∞)(-∞,0][y=x3RR奇Y=x[0,+∞)[0,+∞)非奇非偶[0,+∞)Y=x-1(-∞,0)∪(0,+∞)(-∞,0)∪(0,+∞)奇(-∞,0)(0,+∞)(2)所有幂函数在________上都有定义,并且图象都过点(1,1),且在第____象限无图象.(3)α>0 时,幂函数的图象通过点____________,并且在区间(0,+∞)上是________,α<0 时,幂函数在(0,+∞)上是减函数,图象______原点.自我检测1.如图中曲线是幂函数 y=xn在第一象限的图象.已知 n 取±2,±四个值,则相应于曲线 C1,C2,C3,C4的 n 值依次为________________.2.已知函数:① y=2x;② y=log2x;③ y=x-1;④ y=x.则下列函数图象(在第一象限部分)从左到右依次与函数序号的正确对应顺序是_____________________________________.3.设 α∈{-1,1,,3},则使函数 y=xα的定义域为 R 且为奇函数的所有 α 值为________.4.与函数 y=的图象形状一样的是________(填序号).①y=2x;② y=log2x;③ y=;④ y=x+1.5.已知点(,3)在幂函数 f(x)的图象上,则 f(x)的表达式是____________.探究点一 幂函数的定义与图象例 1 已知幂函数 f(x)的图象过点(,2),幂函数 g(x)的图象过点(2,).(1)求 f(x),g(x)的解析式;(2)求当 x 为何值时:① f(x)>g(x);② f(x)=g(x);③ f(x)