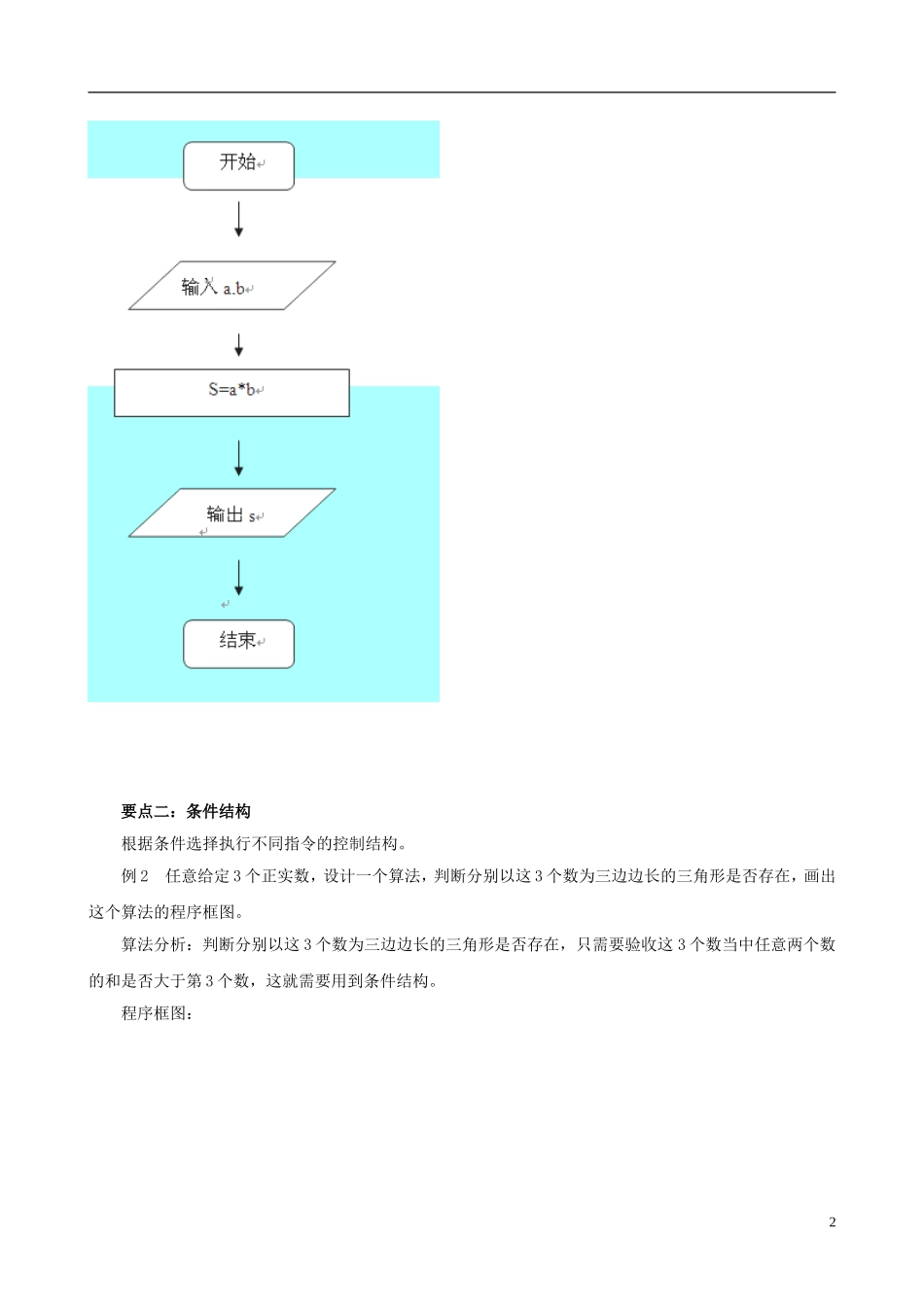
2015 高中数学 1
2 程序框图讲解 新人教 A 版必修 3要点一：顺序结构 顺序结构描述的是是最简单的算法结构，语句与语句之间，框与框之间是按从上到下的顺序进行的
例 1 已知一个三角形的三边分别为 2、3、4，利用海伦公式设计一个算法，求出它的面积，并画出算法的程序框图
算法分析：这是一个简单的问题，只需先算出 p 的值，再将它代入公式，最后输出结果，只用顺序结构就能够表达出算法
J解：程序框图： 2 点评：顺序结构是由若干个依次执行的步骤组成的，是任何一个算法都离不开的基本结构
变式训练 1：输入矩形的边长求它的面积，画出程序框图
1p=(2+3+4)/2222开始s=√p(p-2)(p-3)(p-4)输出 s结束要点二：条件结构根据条件选择执行不同指令的控制结构
例 2 任意给定 3 个正实数，设计一个算法，判断分别以这 3 个数为三边边长的三角形是否存在，画出这个算法的程序框图
算法分析：判断分别以这 3 个数为三边边长的三角形是否存在，只需要验收这 3 个数当中任意两个数的和是否大于第 3 个数，这就需要用到条件结构
程序框图：2点评：条件结构的显著特点是根据不同的选择有不同的流向
变式训练 2：求 x 的绝对值，画出程序框图
3要点三：循环结构在一些算法中，经常会出现从某处开始，按照一定条件，反复执行某一处理步骤的情况，这就是循环结构，反复执行的处理步骤为循环体，显然，循环结构中一定包含条件结构
循环结构分为两类：（1）一类是当型循环结构，如图（1）所示，它的功能是当给定的条件 P1成立时，执行 A 框，A 框执行完毕后，再判断条件 P1是否成立，如果仍然成立，再执行 A 框，如此反复执行 A 框，直到某一次条件 P1不成立为止，此时不再执行 A 框，从 b 离开循环结构
（2）另一类是直到型循环结构，如图（2 所示，它的功能是先执行，然后判断给定的条
