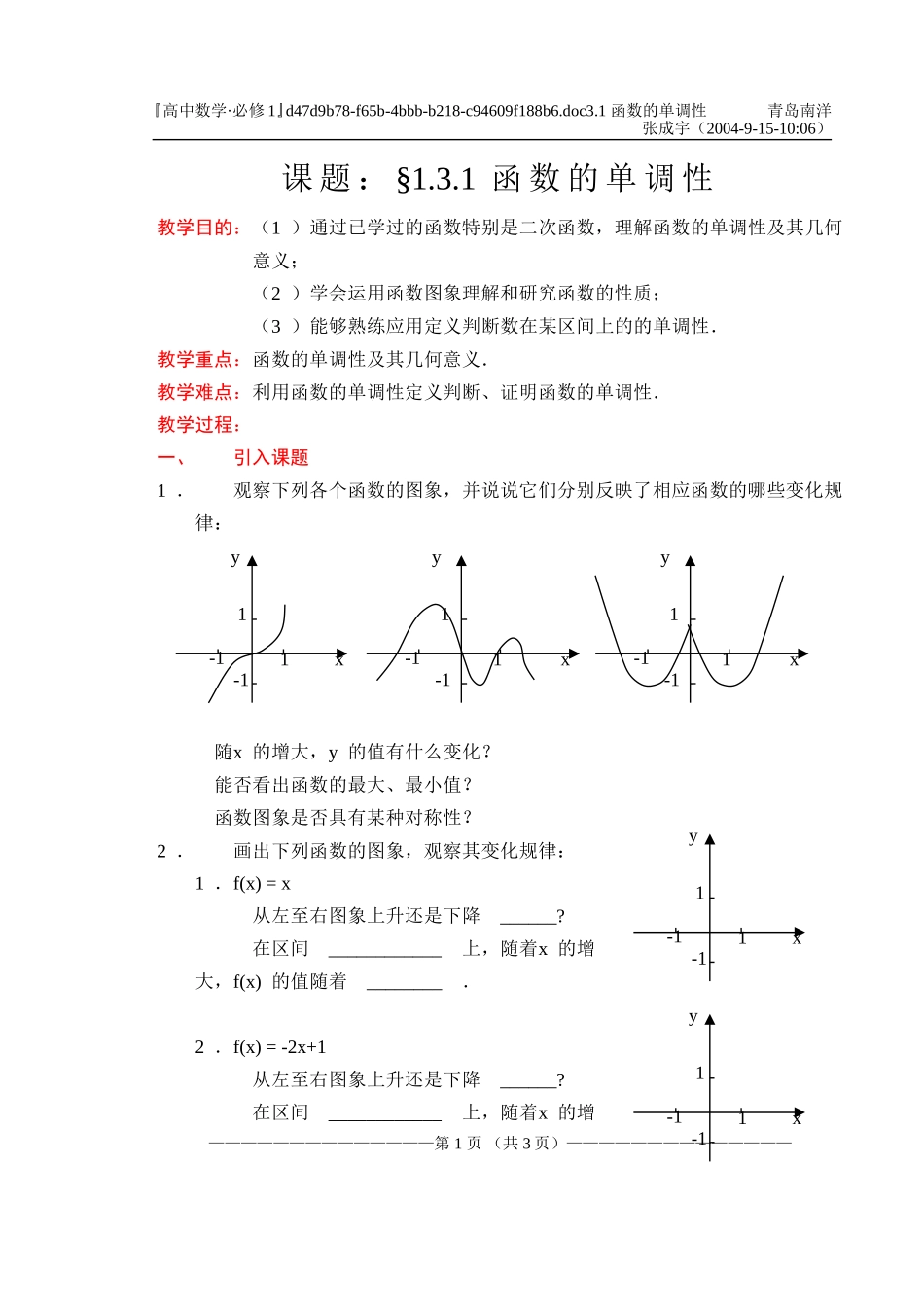
『高中数学·必修 1』d47d9b78-f65b-4bbb-b218-c94609f188b6.doc3.1 函数的单调性 青岛南洋 张成宇(2004-9-15-10:06)课 题 : §1.3.1 函 数 的 单 调 性教学目的:(1 )通过已学过的函数特别是二次函数,理解函数的单调性及其几何意义;(2 )学会运用函数图象理解和研究函数的性质;(3 )能够熟练应用定义判断数在某区间上的的单调性.教学重点:函数的单调性及其几何意义.教学难点:利用函数的单调性定义判断、证明函数的单调性. 教学过程:一、引入课题1 .观察下列各个函数的图象,并说说它们分别反映了相应函数的哪些变化规律: 随x 的增大,y 的值有什么变化? 能否看出函数的最大、最小值? 函数图象是否具有某种对称性?2 .画出下列函数的图象,观察其变化规律:1 .f(x) = x 从左至右图象上升还是下降 ______? 在区间 ____________ 上,随着x 的增大,f(x) 的值随着 ________ .2 .f(x) = -2x+1 从左至右图象上升还是下降 ______? 在区间 ____________ 上,随着x 的增——————————————第 1 页 (共 3 页)——————————————yx1-11-1yx1-11-1yx1-11-1yx1-11-1yx1-11-1『高中数学·必修 1』d47d9b78-f65b-4bbb-b218-c94609f188b6.doc3.1 函数的单调性 青岛南洋 张成宇(2004-9-15-10:06)大,f(x) 的值随着 ________ .3 .f(x) = x2在区间 ____________ 上,f(x) 的值随着x 的增大而 ________ . 在区间 ____________ 上,f(x) 的值随着x 的增大而 ________ .二、新课教学(一)函数单调性定义1 .增函数一般地,设函数y=f(x) 的定义域为I ,如果对于定义域I 内的某个区间D 内的任意两个自变量x1 ,x2 ,当x1