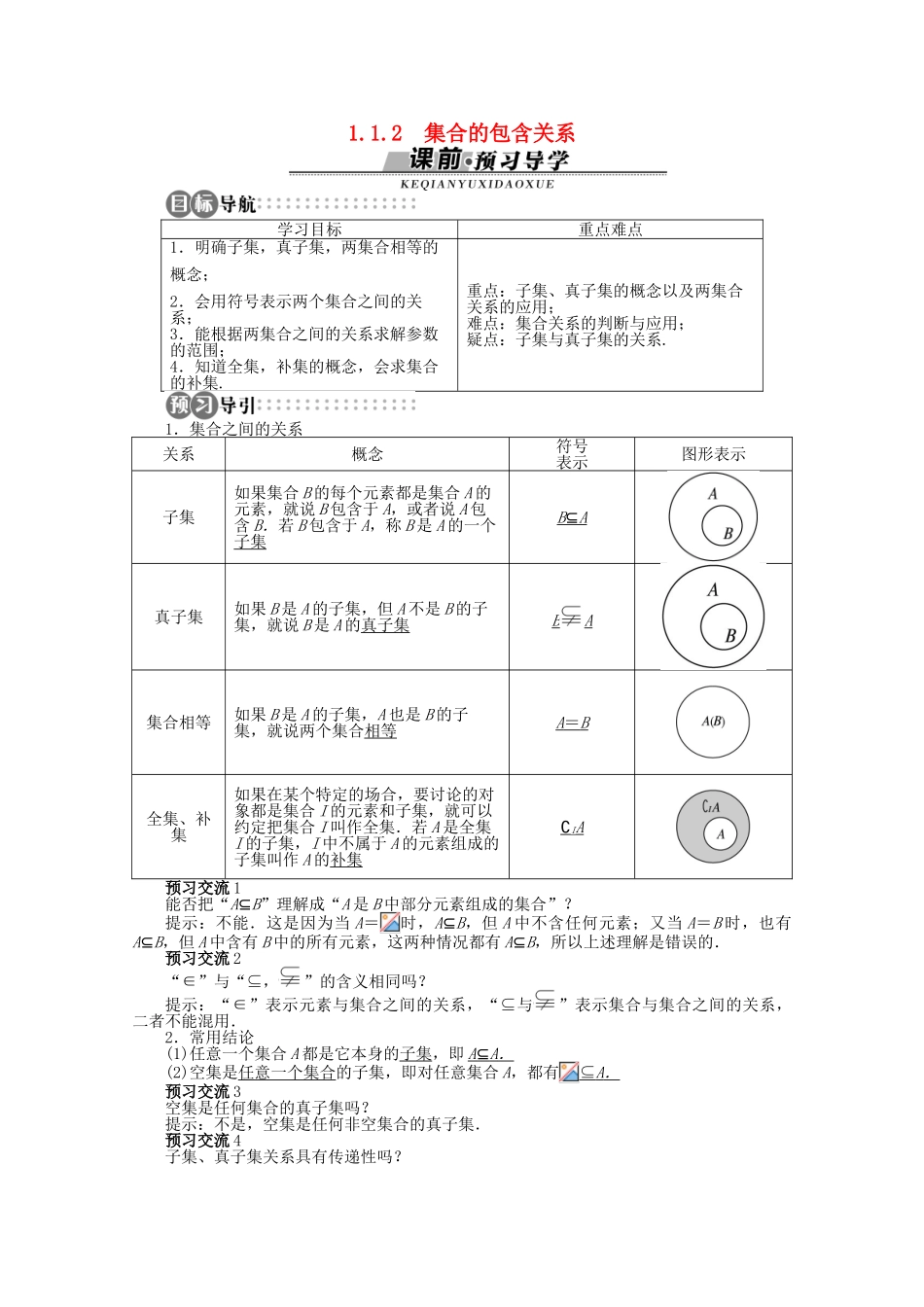
1.1.2 集合的包含关系学习目标重点难点1.明确子集,真子集,两集合相等的概念;2.会用符号表示两个集合之间的关系;3.能根据两集合之间的关系求解参数的范围;4.知道全集,补集的概念,会求集合的补集.重点:子集、真子集的概念以及两集合关系的应用;难点:集合关系的判断与应用;疑点:子集与真子集的关系.1.集合之间的关系关系概念符号表示图形表示子集如果集合 B 的每个元素都是集合 A 的元素,就说 B 包含于 A,或者说 A 包含 B.若 B 包含于 A,称 B 是 A 的一个子集B ⊆ A 真子集如果 B 是 A 的子集,但 A 不是 B 的子集,就说 B 是 A 的真子集BA集合相等如果 B 是 A 的子集,A 也是 B 的子集,就说两个集合相等A = B 全集、补集如果在某个特定的场合,要讨论的对象都是集合 I 的元素和子集,就可以约定把集合 I 叫作全集.若 A 是全集I 的子集,I 中不属于 A 的元素组成的子集叫作 A 的补集∁IA预习交流 1能否把“A⊆B”理解成“A 是 B 中部分元素组成的集合”?提示:不能.这是因为当 A=时,A⊆B,但 A 中不含任何元素;又当 A=B 时,也有A⊆B,但 A 中含有 B 中的所有元素,这两种情况都有 A⊆B,所以上述理解是错误的.预习交流 2“∈”与“⊆,”的含义相同吗?提示:“∈”表示元素与集合之间的关系,“⊆与”表示集合与集合之间的关系,二者不能混用.2.常用结论(1)任意一个集合 A 都是它本身的子集,即 A ⊆ A . (2)空集是任意一个集合的子集,即对任意集合 A,都有⊆ A . 预习交流 3空集是任何集合的真子集吗?提示:不是,空集是任何非空集合的真子集.预习交流 4子集、真子集关系具有传递性吗?提示:具有传递性.若 A⊆B,B⊆C,则 A⊆C;若 AB,BC;则 AC.预习交流 5若全集是 I,那么,I 的补集分别是什么?A 的补集的补集是什么?提示:的补集是 I,I 的补集是,即∁I=I,∁II=,A 的补集的补集是它自身,即∁I(∁IA)=A.一、子集、真子集的确定与集合关系的判断(1)写出集合 A={x|x(x-1)(x2-1)=0}的所有子集,并指出哪些是真子集?(2)若 M={x|x=2n,n∈N},N={x|x=4n,n∈N},试判断 M 与 N 的关系.思路分析:(1)首先确定出集合 A 中的所有元素,然后按元素个数分类写出子集,注意不要忘记;(2)通过列举出 M 与 N 中的元素分析判断二者的关系,或者通过表达式分析两个集合的元素之间的...