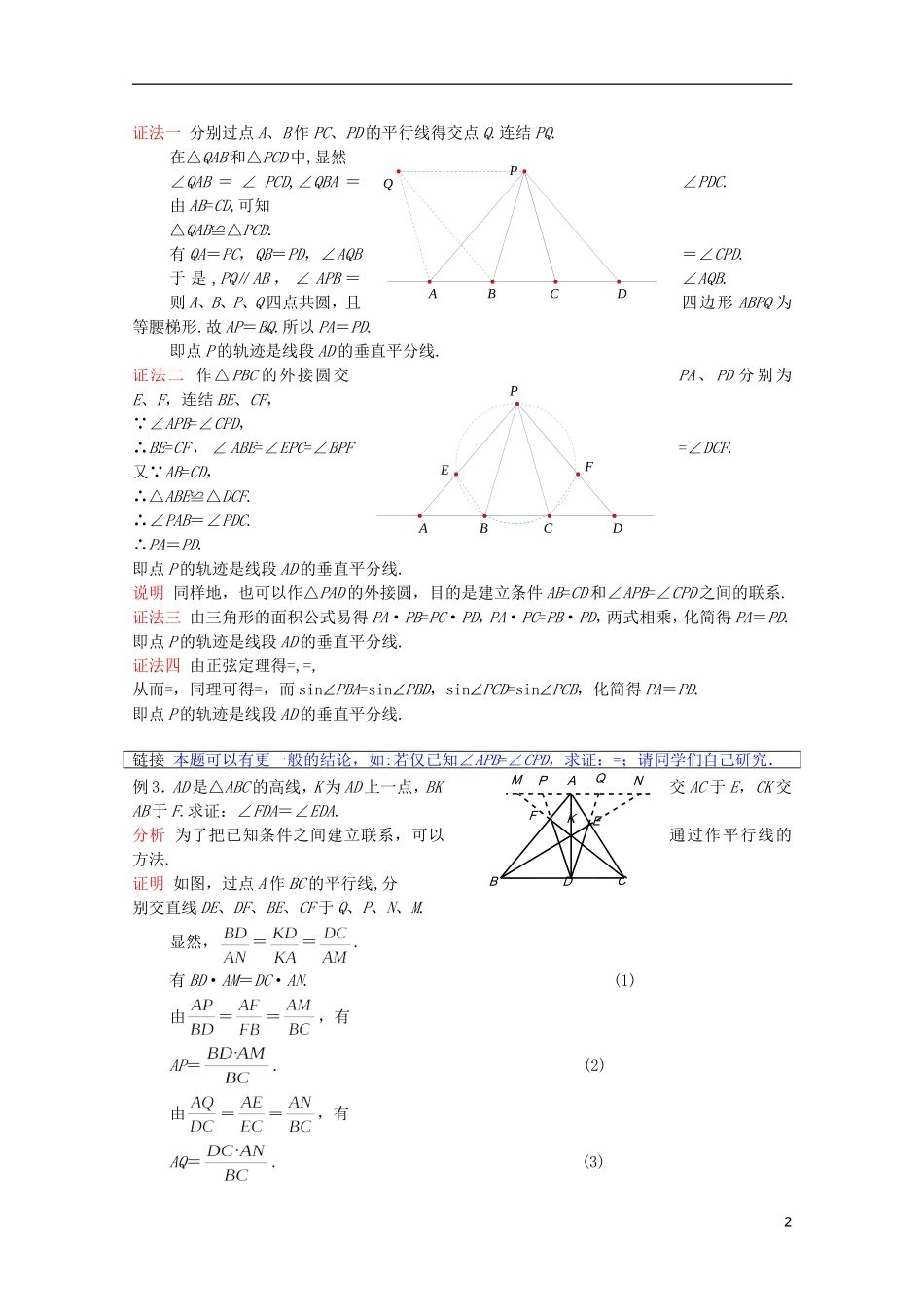
第 16 讲 平几问题选讲平面几何在高中竞赛和国际竞赛中占有重要的地位,本讲将对平几中的一些典型问题的选讲,强化解平几问题的典型思想方法.A 类例题 例 1 如图,已知正方形 ABCD,点 E、F 分别在 BC 、 CD 上 , 且BE+DF=EF,试求∠EAF 的度数.(1989 年全国冬令营)分析 注意到 BE+DF=EF,很容易想到“截长补短”的方法.解 延长 CB 到 F',使得 BF'= DF,连结AF'显然AF'B≌AFD. ∴∠BAF'=∠DAF,AF'=AF.又 EF'=BE+BF'=BE+DF,AE 为公共边,∴AF'E≌AFE.∴∠EAF'=∠EAF.又 ∠FAF'=∠BAD=90º,∴∠EAF=45º.说明 本题AF'B 可以看作是AFD 顺时针旋转 90º 得到的;本题也可以延长 CD 或旋转ABE.例 2 如图,A、B、C、D 为直线上四点,且 AB=CD,点P 为一动点,若∠APB=∠CPD,试求点 P的 轨 迹 .(1989 年全国初中数学联赛)分析 由于已知的两个条件 AB=CD和∠APB=∠CPD,分散在两个三角形中,需要把它们集中,于是可以进行平移或添加辅助圆建立这两个已知条件间的联系.链接 本题若在 EF 上截取 EH=BE,是很难进行下去的,但我们可以用代数的方法来研究,解法如下:过点 A 作 AHEF 于 H,由勾股定理得 AB2+BE2=AH2+EH2,AD2+DF2=AH2+FH2,两式相减可得BE2-DF2=EH2-FH2,于是(BE-DF)(BE+DF)=(EH-FH)(EH+FH),而 BE+DF=EH+FH① 所以 BE-DF=EH-FH②,由①②可得 BE=EH, DF=FH.从而可得 AE 平分∠BAH,AF 平分∠DAH,所以∴∠EAF=45º.HFD CBAE1FDCABEF'FDCABEDABCP证法一 分别过点 A、B 作 PC、PD 的平行线得交点 Q.连结 PQ.在△QAB 和△PCD 中,显然∠QAB = ∠ PCD,∠QBA =∠PDC. 由 AB=CD,可知△QAB≌△PCD.有 QA=PC,QB=PD,∠AQB=∠CPD.于 是 ,PQ∥AB , ∠ APB =∠AQB.则 A、B、P、Q 四点共圆,且四边形 ABPQ 为等腰梯形.故 AP=BQ.所以 PA=PD.即点 P 的轨迹是线段 AD 的垂直平分线.证法二 作△PBC 的外接圆交PA 、 PD 分 别 为E、F,连结 BE、CF, ∠APB=∠CPD,∴BE=CF , ∠ ABE=∠EPC=∠BPF =∠DCF. 又 AB=CD,∴△ABE≌△DCF.∴∠PAB=∠PDC.∴PA=PD.即点 P 的轨迹是线段 AD 的垂直平分线.说明 同样地,也可以作△PAD 的外接圆,目的是建立条件 AB=CD 和∠APB=∠CPD 之间的联系.证法三 由三角形的面积公式易得 PA·PB=PC·PD,PA·PC=PB·PD,两式相乘,化简得 PA=PD....