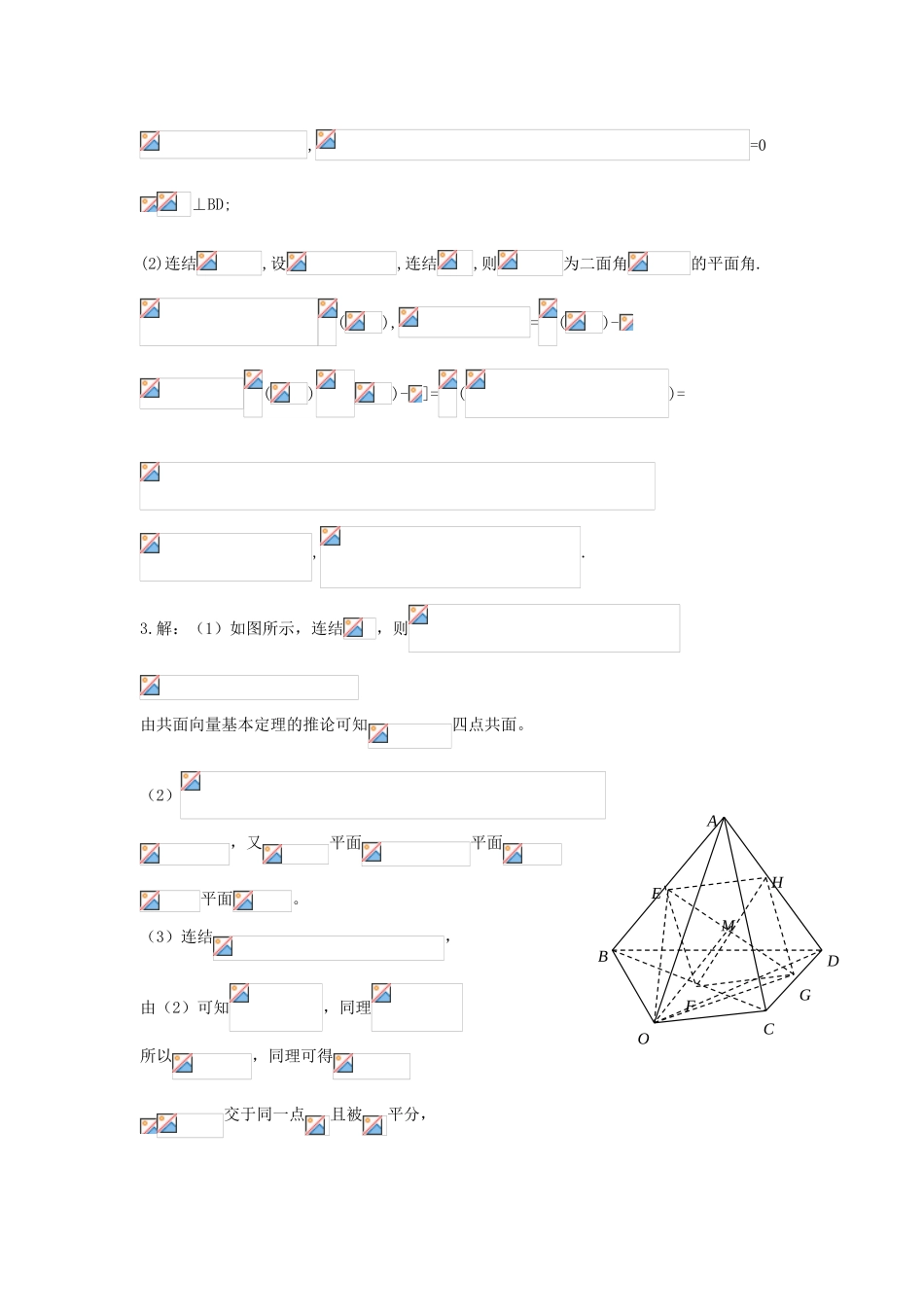
第三章 空间向量与立体几何第一讲 空间向量及其运算[知识梳理][知识盘点]1. 大小和方向 同一向量 相等向量 2. 直线平行或重合 存在实数,使 方向向量3. 同一平面 4. 5. 6. 向量垂直于平面 法向量 [基础闯关]1.D 2.B 3.A 4.D 5. 6.[典例精析]变式训练:1.解:如图所示,连结,则,故.)由已知, 分成的比为 2,故==)于是=()+()=.2.(1)证明:设,则.C1CD1B1A1NMDBA,=0⊥BD;(2)连结,设,连结,则为二面角的平面角.(),=()-())-]=()=,.3.解:(1)如图所示,连结,则由共面向量基本定理的推论可知四点共面。(2),又平面平面平面。(3)连结,由(2)可知,同理所以,同理可得交于同一点且被平分,DGCHMFOBEA4.解:(1)设侧棱长为 b,则 A(0,-1,0), B1( ,0,b), B(,0,0), C1(0,1,b) ={,1,b}, ={-,1,b} AB1 ⊥AB1 ∴ -3+1+b2=0, b=(2) (3) 设异面直线 AM 与 BC 所成角为, , ,∴=9005.解:以 D 为原点建立如图所示的坐标系, 设存在点 P(0,0,z),6.解:(1)设,则由题意有:,即.(2)若存在向量与的方向向量共线,则,又,= ( - a , 0 , z ) ,= ( -a,a,0), =(a,a,a), B1D⊥面 PAC,∴·=0,·=0.∴-a2+az=0.∴z=a,即点 P 与 D1重合.∴点 P 与 D1重合时,DB1⊥面 PAC.,这显然是不可能的,所以不存在满足题意的向量. [能力提升]1.C 2.B 3.A 4.B 5.C 6.3a+3b-5c 7.1 或 3 8. 9.0,010 . ( 1 ) 如 图 建 立 空 间 直 角 坐 标 系 , 设, 则. 由得: 由 CP⊥BD,得: ,所以点 P 为的中点时,有 CP⊥BD (2)过 D 作 DE⊥B1C1,垂足为 E,易知 E 为 D 在平面上的射影 ∴∠DPE 为 DP 与平面所成的角 由(1),P(4,0,z),得:.即 DP 与面所成的角的余弦值为.11. 建 立 如 图 所 示 的 空 间 直 角 坐 标 系 D—xyz , 则B(1,1,0),E(1/2,1,1),F(0,1/2,1),设=zyxB1FD1A1DACEC1B(x,y,z)是平面 BDFE 的法向量,由⊥,⊥,=(1,1,0),=(0,1/2,1)得: ·= x+y=0 ·=1/2 y+ z=0所以:x= - y z= 令 y=1,得=(-1,1,1/2),设点 A 在平面 BDFE 上的射影为H,连结 A1D,A1D 是平面 BDFE 的斜线段,则: cos﹤,﹥=所以| cos﹤,﹥=1 所以点 A1到平面 BEFE 的距离为 1(3)由(2)知∠D A1H=45°,∠A1DH 是直线 A1D...