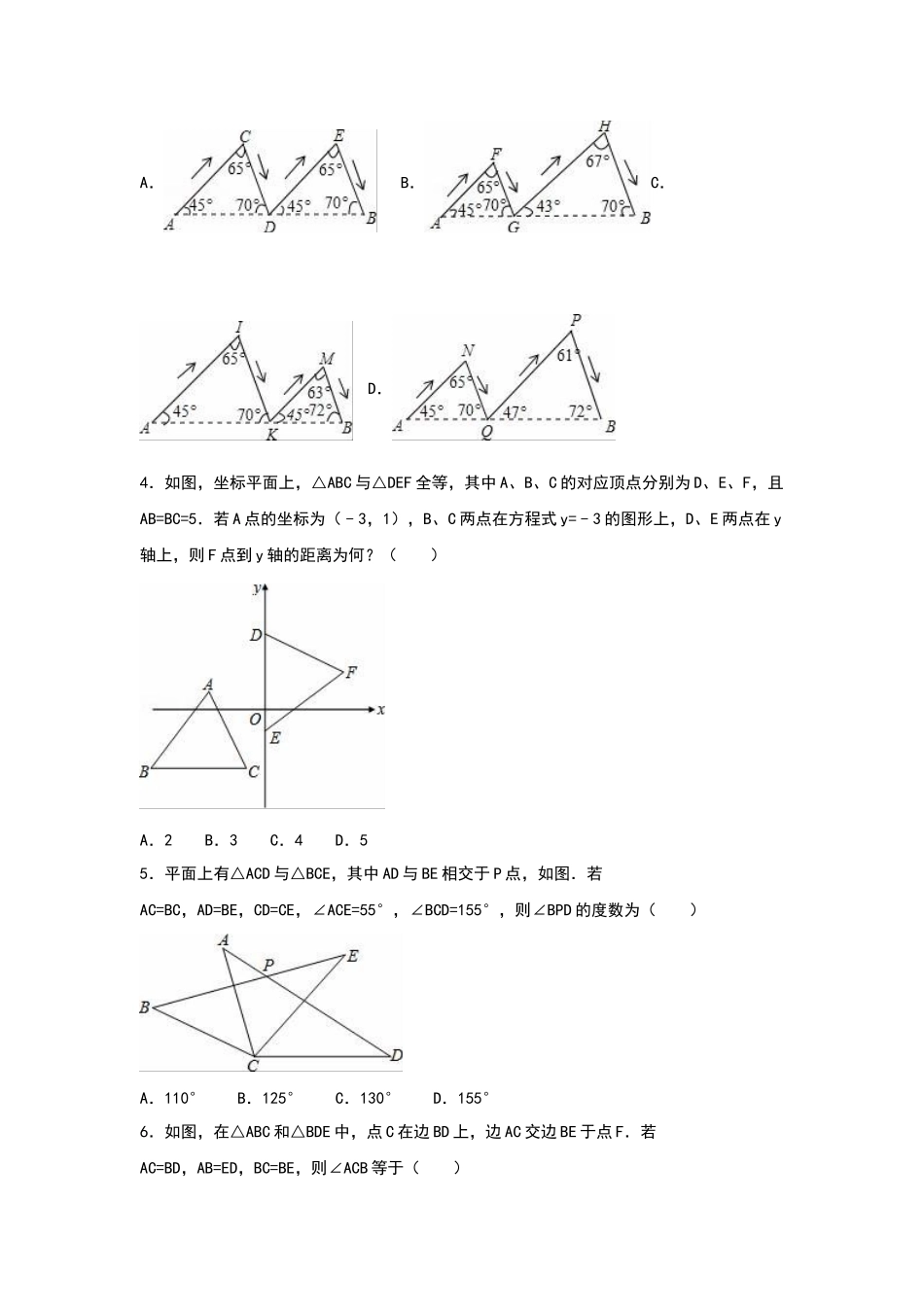
第 12 章 全等三角形一、选择题1.如图,在△ABC 中,∠ABC=45°,AC=8cm,F 是高 AD 和 BE 的交点,则 BF 的长是( )A.4cmB.6cmC.8cmD.9cm2.如图,将正方形 OABC 放在平面直角坐标系中,O 是原点,A 的坐标为(1,),则点C 的坐标为( )A.(﹣,1) B.(﹣1,) C.(,1)D.(﹣,﹣1)3.在连接 A 地与 B 地的线段上有四个不同的点 D、G、K、Q,下列四幅图中的实线分别表示某人从 A 地到 B 地的不同行进路线(箭头表示行进的方向),则路程最长的行进路线图是( )A.B.C.D.4.如图,坐标平面上,△ABC 与△DEF 全等,其中 A、B、C 的对应顶点分别为 D、E、F,且AB=BC=5.若 A 点的坐标为(﹣3,1),B、C 两点在方程式 y=﹣3 的图形上,D、E 两点在 y轴上,则 F 点到 y 轴的距离为何?( )A.2B.3C.4D.55.平面上有△ACD 与△BCE,其中 AD 与 BE 相交于 P 点,如图.若AC=BC,AD=BE,CD=CE,∠ACE=55°,∠BCD=155°,则∠BPD 的度数为( )A.110°B.125°C.130°D.155°6.如图,在△ABC 和△BDE 中,点 C 在边 BD 上,边 AC 交边 BE 于点 F.若AC=BD,AB=ED,BC=BE,则∠ACB 等于( )A.∠EDBB.∠BEDC.∠AFBD.2∠ABF7.如图,AB=4,射线 BM 和 AB 互相垂直,点 D 是 AB 上的一个动点,点 E 在射线 BM 上,BE=DB,作 EF⊥DE 并截取 EF=DE,连结 AF 并延长交射线 BM 于点 C.设 BE=x,BC=y,则 y 关于 x 的函数解析式是( )A.y=﹣B.y=﹣C.y=﹣D.y=﹣8.如图,在四边形 ABCD 中,AB=AD=6,AB⊥BC,AD⊥CD,∠BAD=60°,点 M、N 分别在AB、AD 边上,若 AM:MB=AN:ND=1:2,则 tan∠MCN=( )A.B.C.D.﹣29.如图,点 E 在正方形 ABCD 的对角线 AC 上,且 EC=2AE,直角三角形 FEG 的两直角边EF、EG 分别交 BC、DC 于点 M、N.若正方形 ABCD 的边长为 a,则重叠部分四边形 EMCN 的面积为( )A. a2 B. a2 C. a2 D. a2 二、解答题(共 21 小题)10.如图,已知 AB∥DE,AB=DE,AF=CD,∠CEF=90°.(1)若∠ECF=30°,CF=8,求 CE 的长;(2)求证:△ABF≌△DEC;(3)求证:四边形 BCEF 是矩形.11.已知△ABC 为等边三角形,D 为 AB 边所在的直线上的动点,连接 DC,以 DC 为边在 DC两侧作等边△DCE 和等边△DCF(点 E 在 DC 的右侧或上侧,点...