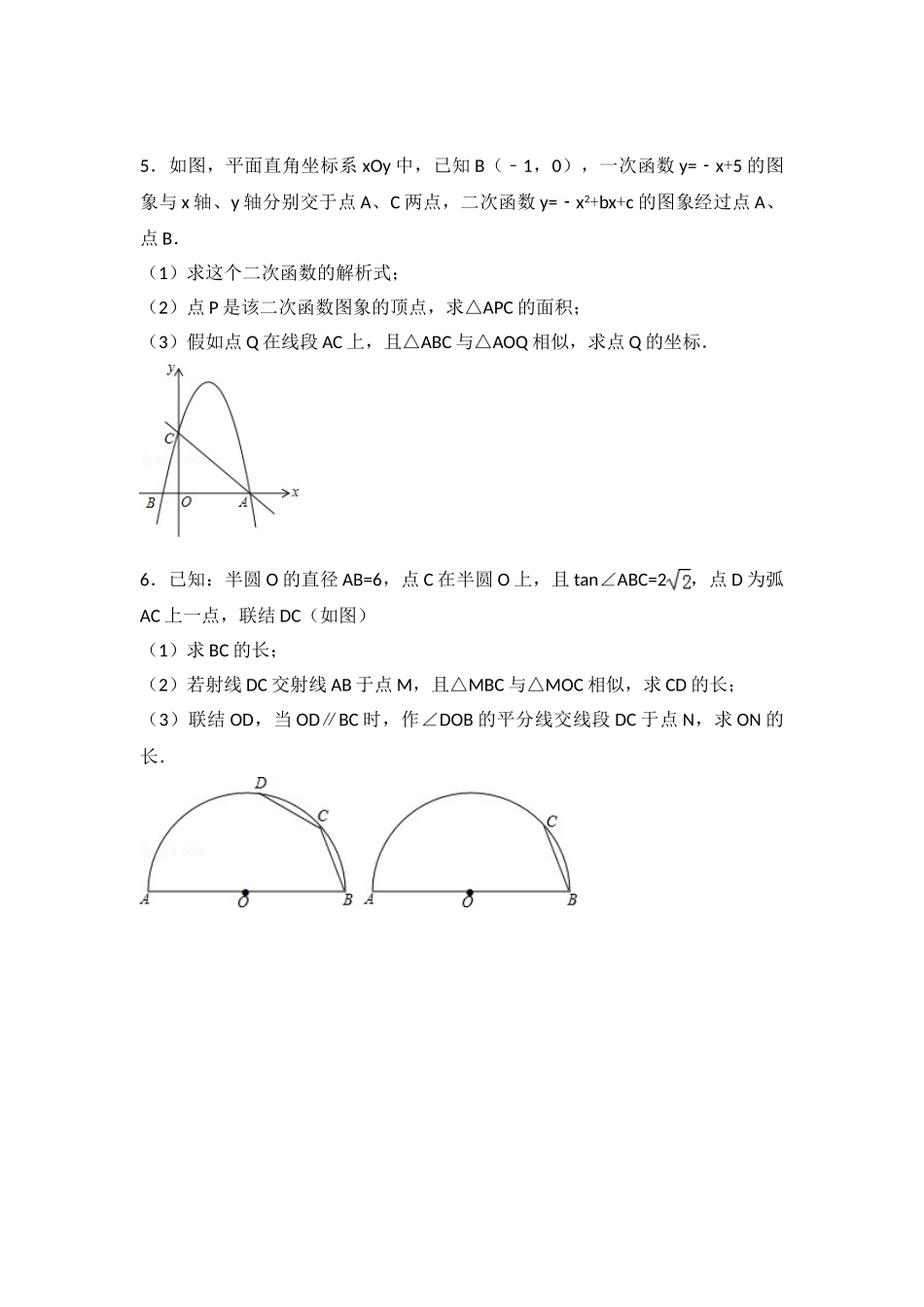
2025 挑战压轴题 中考数学精讲解读篇 因动点产生的相似三角形问题1.如图,在平面直角坐标系 xOy 中,将抛物线 y=x2的对称轴绕着点 P(0,2)顺时针旋转 45°后与该抛物线交于 A、B 两点,点 Q 是该抛物线上一点.(1)求直线 AB 的函数表达式;(2)如图①,若点 Q 在直线 AB 的下方,求点 Q 到直线 AB 的距离的最大值;(3)如图②,若点 Q 在 y 轴左侧,且点 T(0,t)(t<2)是射线 PO 上一点,当以 P、B、Q 为顶点的三角形与△PAT 相似时,求所有满足条件的 t 的值. 2.如图,已知 BC 是半圆 O 的直径,BC=8,过线段 BO 上一动点 D,作 AD⊥BC交半圆 O 于点 A,联结 AO,过点 B 作 BH⊥AO,垂足为点 H,BH 的延长线交半圆 O 于点 F.(1)求证:AH=BD;(2)设 BD=x,BE•BF=y,求 y 关于 x 的函数关系式;(3)如图 2,若联结 FA 并延长交 CB 的延长线于点 G,当△FAE 与△FBG 相似时,求 BD 的长度.3.如图,在平面直角坐标系 xOy 中,直线 AB 过点 A(3,0)、B(0,m)(m>0),tan∠BAO=2.(1)求直线 AB 的表达式;(2)反比例函数 y=的图象与直线 AB 交于第一象限内的 C、D 两点(BD<BC),当 AD=2DB 时,求 k1的值;(3)设线段 AB 的中点为 E,过点 E 作 x 轴的垂线,垂足为点 M,交反比例函数y=的图象于点 F,分别联结 OE、OF,当△OEF∽△OBE 时,请直接写出满足条件的所有 k2的值.4.如图,在 Rt△ABC 中,∠ACB=90°,AC=1,BC=7,点 D 是边 CA 延长线的一点,AE⊥BD,垂足为点 E,AE 的延长线交 CA 的平行线 BF 于点 F,连结 CE 交 AB于点 G.(1)当点 E 是 BD 的中点时,求 tan∠AFB 的值;(2)CE•AF 的值是否随线段 AD 长度的改变而变化?假如不变,求出 CE•AF 的值;假如变化,请说明理由;(3)当△BGE 和△BAF 相似时,求线段 AF 的长.5.如图,平面直角坐标系 xOy 中,已知 B(﹣1,0),一次函数 y=x﹣ +5 的图象与 x 轴、y 轴分别交于点 A、C 两点,二次函数 y=x﹣ 2+bx+c 的图象经过点 A、点 B.(1)求这个二次函数的解析式;(2)点 P 是该二次函数图象的顶点,求△APC 的面积;(3)假如点 Q 在线段 AC 上,且△ABC 与△AOQ 相似,求点 Q 的坐标.6.已知:半圆 O 的直径 AB=6,点 C 在半圆 O 上,且 tan∠ABC=2,点 D 为弧...