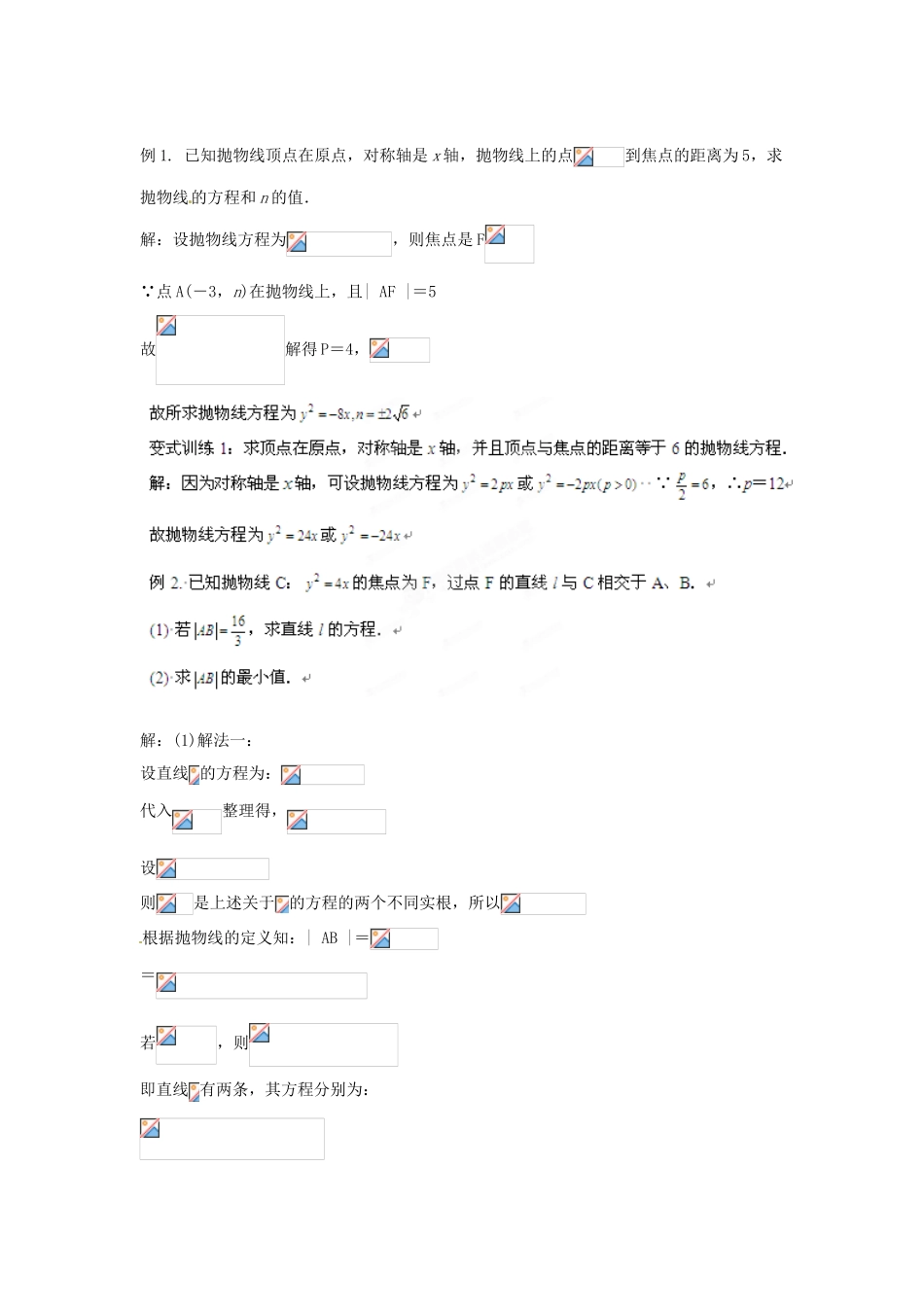
福建省长泰一中高考数学一轮复习《抛物线》学案3.抛物线的几何性质:对进行讨论.① 点的范围: 、 .② 对称性:抛物线关于 轴对称.③ 离心率 .④ 焦半径公式:设 F 是抛物线的焦点,是抛物线上一点,则 .⑤ 焦点弦长公式:设 AB 是过抛物线焦点的一条弦(焦点弦)i) 若,,则= , .ii) 若 AB 所在直线的倾斜角为(则= .特别地,当时,AB 为抛物线的通径,且= .iii) S△AOB= (表示成 P 与 θ 的关系式).iv) 为定值,且等于 .典型例题基础过关例 1. 已知抛物线顶点在原点,对称轴是 x 轴,抛物线上的点到焦点的距离为 5,求抛物线的方程和 n 的值.解:设抛物线方程为,则焦点是 F 点 A(-3,n)在抛物线上,且| AF |=5故解得 P=4,解:(1)解法一:设直线 的方程为:代入整理得,设则是上述关于的方程的两个不同实根,所以根据抛物线的定义知:| AB |==若,则即直线 有两条,其方程分别为:解法二:由抛物线的焦点弦长公式|AB|=(θ 为 AB 的倾斜角)易知 sinθ=±,即直线 AB 的斜率 k=tanθ=±,故所求直线方程为:或.(2) 由(1)知,当且仅当时,|AB|有最小值 4.解法二:由(1)知|AB|==∴ |AB|min=4 (此时 sinθ=1,θ=90°)变式训练 2:过抛物线 y2=4x 的焦点作一条直线与抛物线相交于 A、B 两点,它们的横坐标之和等于 5,则这样的直线( )A.有且仅有一条 B.有且仅有两条C.有无数条D.不存在解:B例 3. 若 A(3,2),F 为抛物线的焦点,P 为抛物线上任意一点,求的最小值及取得最小值时的 P 的坐标.解:抛物线的准线方程为过 P 作 PQ 垂直于准线于 Q 点,由抛物线定义得|PQ|=| PF |,∴| PF |+| PA |=| PA |+| PQ |要使| PA |+| PQ |最小,A、P、Q 三点必共线,即 AQ 垂直于准线,AQ 与抛物线的交点为P 点从而|PA|+|PF|的最小值为此时 P 的坐标为(2,2)变式训练 3:一个酒杯的轴截面是抛物线的一部分,它的方程是 x2,在杯内放入一个玻璃球,要使球触及酒杯底部,则玻璃球的半径 r 的取值范围是 。解:例 4. 设 A(x1,y1),B(x2,y2),两点在抛物线 y=2x2上,l 是 AB 的垂直平分线.(1)当且仅当 x1+x2取何值时,直线 l 经过抛物线的焦点 F?证明你的结论?(2)当直线 l 的斜率为 2 时,求在 y 轴上的截距的取值范围.解:(1)F∈l|FA|=|FB|A、B 两点到抛物线的准线的距离相...