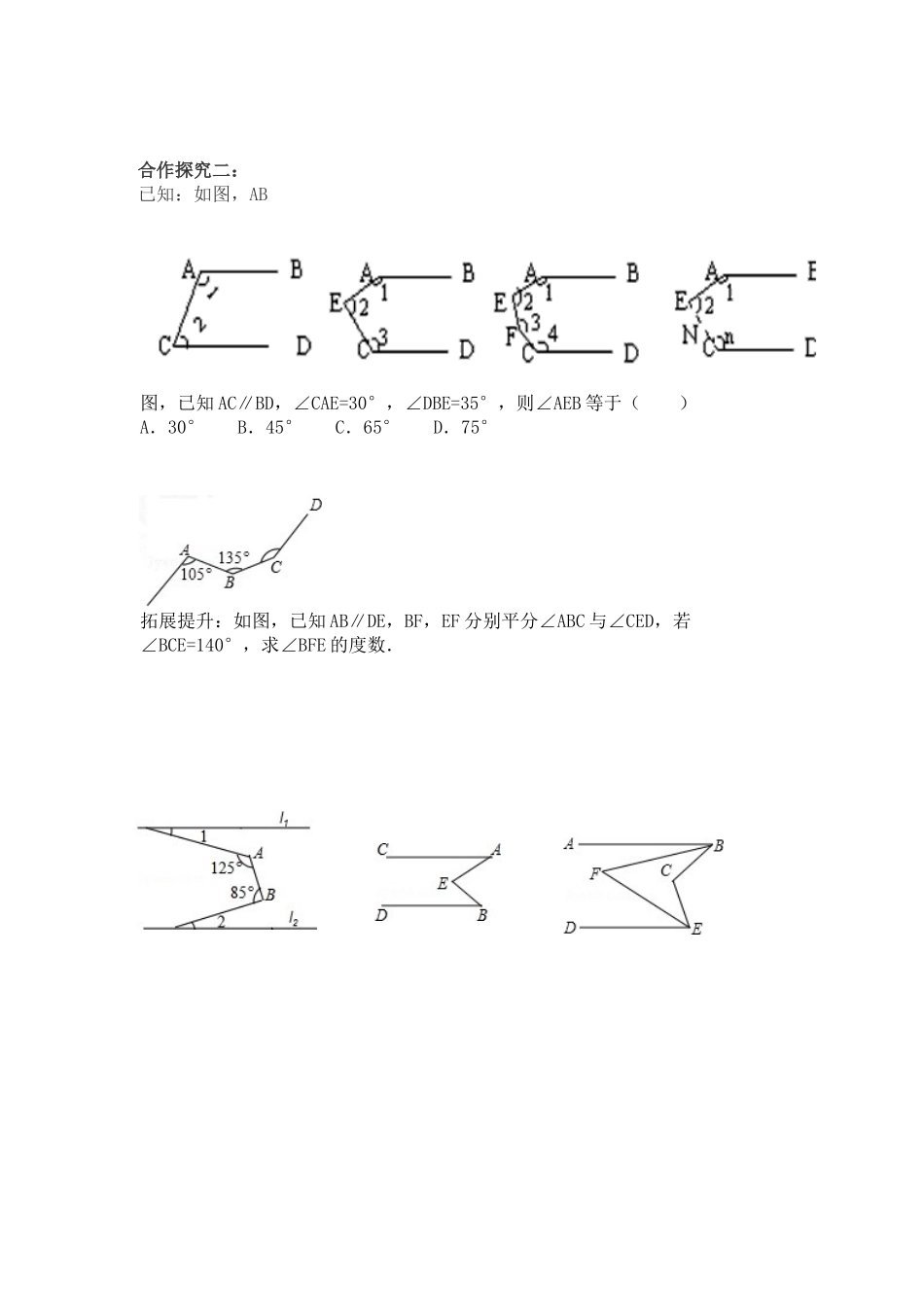
平行线中的拐点问题学习目标:1.能正确解决常见的拐点问题。2.灵活应用平行线的性质与判定解决相关问题。复习回顾:1.如图(1),ABA、1800 B、 2700 C、 3600 D、54002.如图(2),AB∥CD,则 x,y,z 之间的关系是( )A、x+y+z=360°B、x-y+z=180°C、x+y-z=180°D、y+z-x=180°A EC D方法指导:解决平行线中的拐点问题,常用方法为:根据题目中已知的平行线和“拐点“的情况,在“拐点”处作已知平行线的平行线,然后根据平行线的性质得到相应的结论。合作探究一:(1)已知:如图 1,AB∥CD,求证:∠B+∠D=∠BED;(2)已知:如图 2,AB∥CD,试探求∠B、∠D 与∠E 之间的数量关系,并说明理由.(3)已知:如图 3,AB∥CD,试探求∠B、∠D 与∠E 之间的数量关系,并说明理由. B合作探究二:已知:如图,AB图,已知 AC∥BD,∠CAE=30°,∠DBE=35°,则∠AEB 等于( )A.30°B.45°C.65°D.75°拓展提升:如图,已知 AB∥DE,BF,EF 分别平分∠ABC 与∠CED,若∠BCE=140°,求∠BFE 的度数.