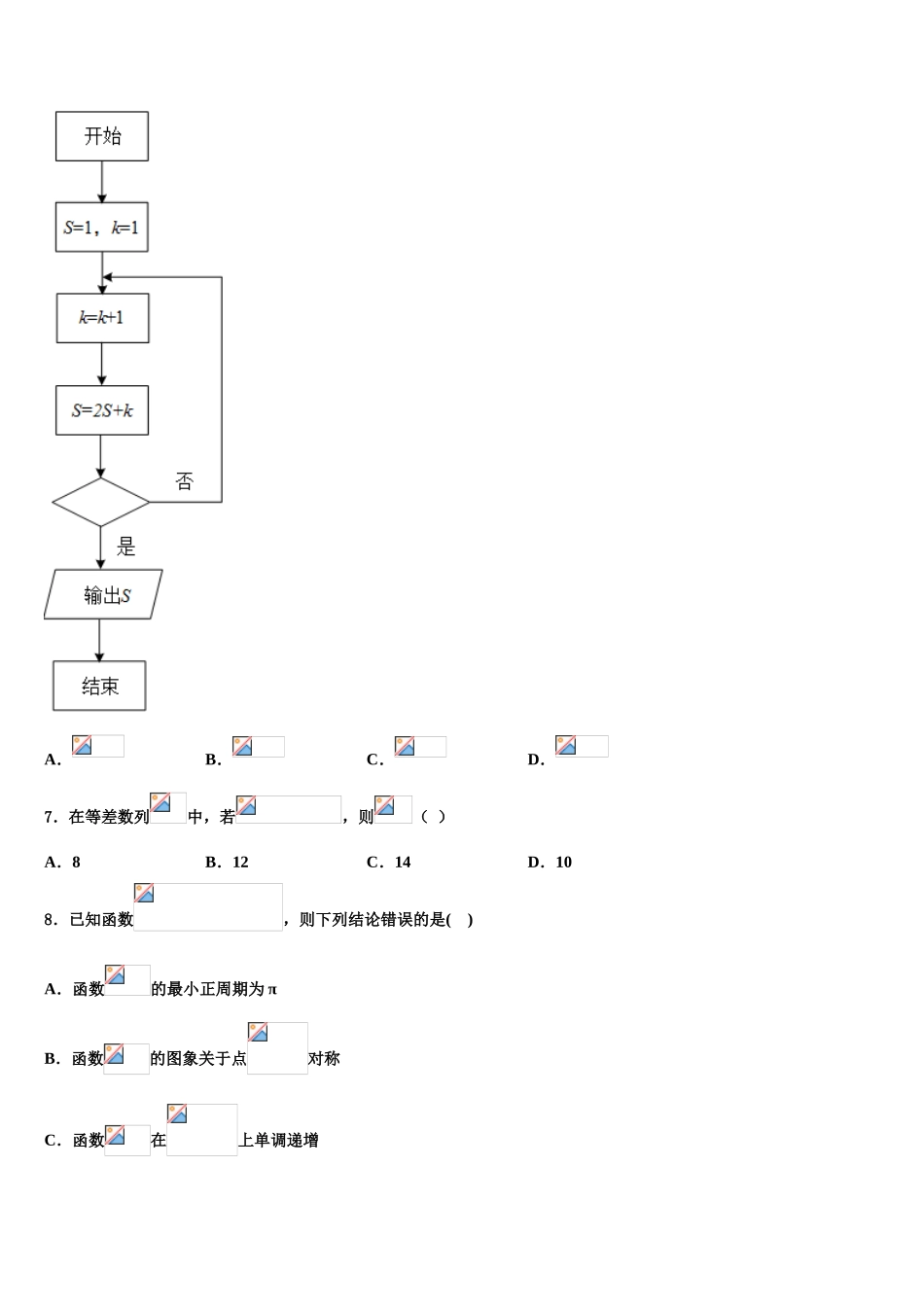
2025-2025 高考数学模拟试卷含解析注意事项1.考生要仔细填写考场号和座位序号。2.试题所有答案必须填涂或书写在答题卡上,在试卷上作答无效。第一部分必须用 2B 铅笔作答;第二部分必须用黑色字迹的签字笔作答。3.考试结束后,考生须将试卷和答题卡放在桌面上,待监考员收回。一、选择题:本题共 12 小题,每小题 5 分,共 60 分。在每小题给出的四个选项中,只有一项是符合题目要求的。1.已知随机变量满足,,.若,则( )A.,B.,C.,D.,2.如图,四面体中,面和面都是等腰直角三角形,,,且二面角的大小为,若四面体的顶点都在球上,则球的表面积为( )A.B.C.D.3.设函数在上可导,其导函数为,若函数在处取得极大值,则函数的图象可能是( )A.B.C.D.4.设复数满足,则( )A.B.C.D.5.如图所示,已知某几何体的三视图及其尺寸(单位:),则该几何体的表面积为( )A. B.C.D.6.某程序框图如图所示,若输出的,则推断框内为( )A.B.C.D.7.在等差数列中,若,则( )A.8B.12C.14D.108.已知函数,则下列结论错误的是( )A.函数的最小正周期为 πB.函数的图象关于点对称C.函数在上单调递增D.函数的图象可由的图象向左平移个单位长度得到9. 的内角的对边分别为,已知,则角的大小为( )A.B.C.D.10.已知,是椭圆的左、右焦点,过的直线交椭圆于两点.若依次构成等差数列,且,则椭圆的离心率为A.B.C.D.11.已知,,分别为内角,,的对边,,,的面积为,则( )A.B.4C.5D.12.记单调递增的等比数列的前项和为,若,,则( )A.B.C.D.二、填空题:本题共 4 小题,每小题 5 分,共 20 分。13.西周初数学家商高在公元前 1000 年发现勾股定理的一个特例:勾三,股四,弦五.此发现早于毕达哥拉斯定理五百到六百年.我们把可以构成一个直角三角形三边的一组正整数称为勾股数.现从 3,4,5,6,7,8,9,10,11,12,13 这 11 个数中随机抽取 3 个数,则这 3 个数能构成勾股数的概率为__________.14.已知点 M 是曲线 y=2lnx+x23﹣ x 上一动点,当曲线在 M 处的切线斜率取得最小值时,该切线的方程为_______.15.两光滑的曲线相切,那么它们在公共点处的切线方向相同.如图所示,一列圆 (an>0,rn>0,n=1,2…)逐个外切,且均与曲线 y=x2相切,若 r1=1,则 a1=___,rn=______16.设满足约束条件,则的取值范围是______.三、解答题:共 70 分。解...