高考数学 考点一遍过 专题01 集合（含解析）理试题VIP免费

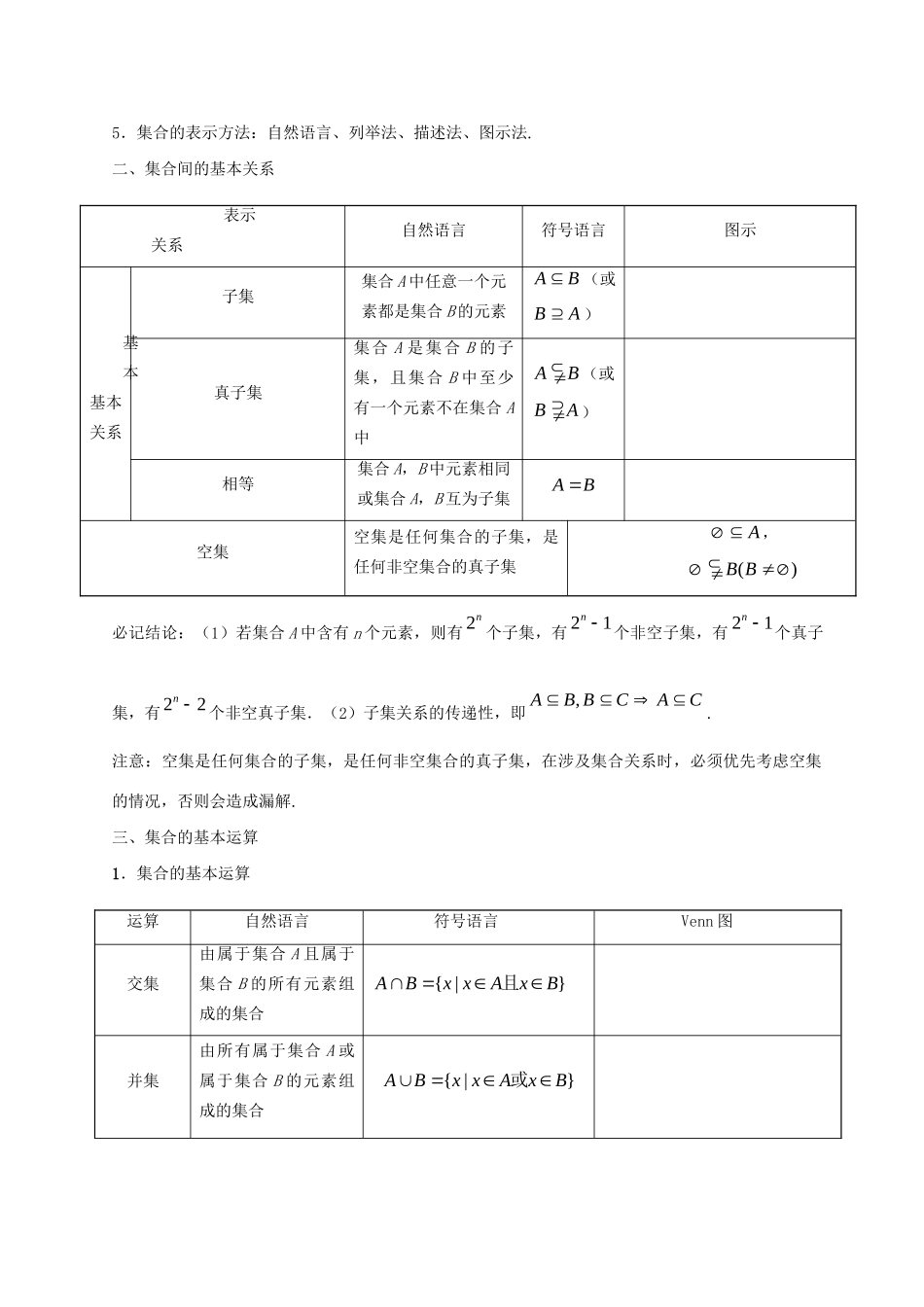
考点01集合1．集合的含义与表示（1）了解集合的含义，体会元素与集合的属于关系.（2）能用自然语言、图形语言、集合语言（列举法或描述法）描述不同的具体问题.2．集合间的基本关系（1）理解集合之间包含与相等的含义，能识别给定集合的子集.（2）在具体情境中，了解全集与空集的含义.3．集合的基本运算（1）理解两个集合的并集与交集的含义,会求两个简单集合的并集与交集.（2）理解在给定集合中一个子集的补集的含义，会求给定子集的补集.（3）能使用韦恩（Venn）图表达集合间的基本关系及集合的基本运算.一、集合的基本概念1．元素与集合的关系：aAaA属于，记为不属于，记为.2．集合中元素的特征：确定性一个集合中的元素必须是确定的，即一个集合一旦确定，某一个元素要么是该集合中的元素，要么不是，二者必居其一，这个特性通常被用来判断涉及的总体是否能构成集合互异性集合中的元素必须是互异的．对于一个给定的集合，它的任何两个元素都是不同的．这个特性通常被用来判断集合的表示是否正确，或用来求集合中的未知元素无序性集合与其中元素的排列顺序无关，如a，b，c组成的集合与b，c，a组成的集合是相同的集合．这个特性通常被用来判断两个集合的关系3．集合的分类：有限集与无限集，特别地，我们把不含有任何元素的集合叫做空集，记作.4．常用数集及其记法：集合非负整数集(自然数集)正整数集整数集有理数集实数集复数集符号NN或+NZQRC注意：实数集R不能表示为{x|x为所有实数}或{R}“，因为{}”“”“”包含所有全体的含义.5．集合的表示方法：自然语言、列举法、描述法、图示法.二、集合间的基本关系表示关系自然语言符号语言图示基本基本关系子集集合A中任意一个元素都是集合B的元素AB（或BA）真子集集合A是集合B的子集，且集合B中至少有一个元素不在集合A中AB（或BA）相等集合A，B中元素相同或集合A，B互为子集AB空集空集是任何集合的子集，是任何非空集合的真子集A，()BB必记结论：（1）若集合A中含有n个元素，则有2n个子集，有21n个非空子集，有21n个真子集，有22n个非空真子集．（2）子集关系的传递性，即,ABBCAC.注意：空集是任何集合的子集，是任何非空集合的真子集，在涉及集合关系时，必须优先考虑空集的情况，否则会造成漏解.三、集合的基本运算1．集合的基本运算运算自然语言符号语言Venn图交集由属于集合A且属于集合B的所有元素组成的集合{|}ABxxAxB且并集由所有属于集合A或属于集合B的元素组成的集合|}{ABxxAxB或补集由全集U中不属于集合A的所有元素组成的集合{|}UAxxUxA且ð2．集合运算的相关结论交集ABAABBAAAAABBA并集ABAABBAAAAAABBA补集()UUAAððUUðUUð()UAAð()UAAUð3．必记结论(.)UUUABABAABBABABððð考向一集合的基本概念解决集合概念问题的一般思路：（1）研究集合问题时，首先要明确构成集合的元素是什么，即弄清该集合是数集、点集，还是其他集合，然后再看集合的构成元素满足的限制条件是什么，从而准确把握集合的意义．常见的集合的意义如下表：集合{0|}xfx{0|}xfx{|}xyfx{|}yyfx{(,)|}yxyfx集合的意义方程0fx的解集不等式0fx的解集函数yfx的定义域函数yfx的值域函数yfx图象上的点集（2）利用集合元素的限制条件求参数的值或确定集合中的元素的个数时，要注意检验集合是否满足元素的互异性.典例1设集合{1,2,4}A，集合{|,,}BxxabaAbA，则集合B中元素的个数是A．B．C．D．【答案】C【名师点睛】在解题时经常用到集合元素的互异性，一方面利用集合元素的互异性能顺利找到解题的切入点；另一方面，在解答完毕时，注意检验集合的元素是否满足互异性，以确保答案正确．1．已知集合{1,2,3,4,5}A,{(,)|,,}BxyxAyAxyA,则B中所含元素的个数为A．3B．6C．8D．10考向二集合间的基本关系集合间的基本关系在高考中时有出现，常考查求子集、真子集的个数及利用集合关系求参...