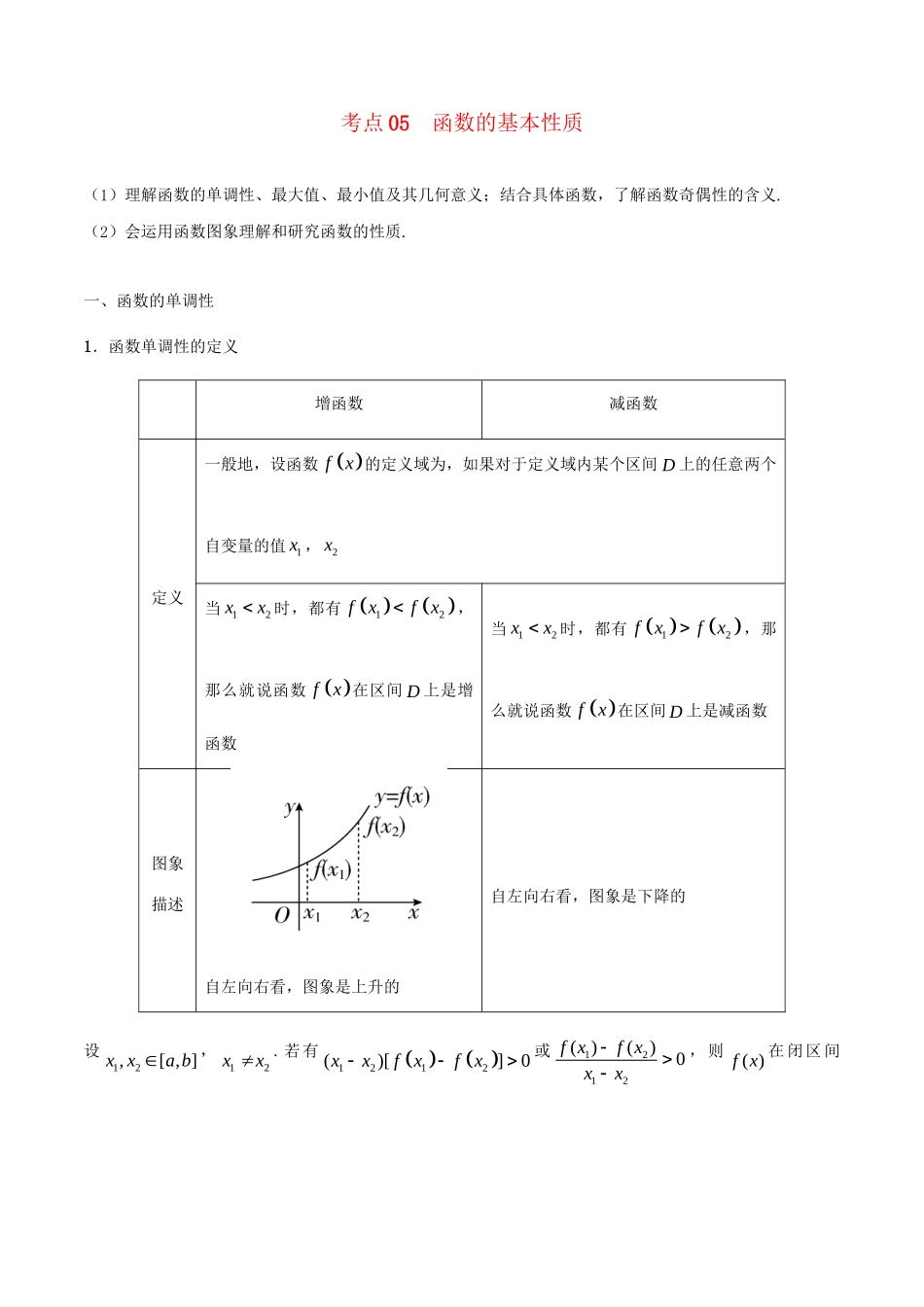
考点05函数的基本性质(1)理解函数的单调性、最大值、最小值及其几何意义;结合具体函数,了解函数奇偶性的含义.(2)会运用函数图象理解和研究函数的性质.一、函数的单调性1.函数单调性的定义增函数减函数定义一般地,设函数fx的定义域为,如果对于定义域内某个区间D上的任意两个自变量的值1x,2x当12xx时,都有12fxfx,那么就说函数fx在区间D上是增函数当12xx时,都有12fxfx,那么就说函数fx在区间D上是减函数图象描述自左向右看,图象是上升的自左向右看,图象是下降的设12,[,]xxab,12xx.若有1212()0[]xxfxfx或1212()()0fxfxxx,则()fx在闭区间[],ab上是增函数;若有1212()0[]xxfxfx或1212()()0fxfxxx,则()fx在闭区间[],ab上是减函数.此为函数单调性定义的等价形式.2.单调区间的定义若函数yfx在区间D上是增函数或减函数,则称函数yfx在这一区间上具有(严格的)单调性,区间D叫做函数fx的单调区间.注意:(1)“”单调性是与区间紧密相关的概念,一个函数在不同的区间上,可以有不同的单调性,同一种“”“”“”单调区间用和或,连接,不能用∪连接.(2)函数的单调性只能在函数的定义域内来讨论,所以求函数的单调区间,必须先求函数的定义域.(3“)函数的单调区间是A”“与函数在区间B”上单调是两个不同的概念,注意区分,显然BA.(4)函数的单调性是对某个区间而言的,所以要受到区间的限制.例如函数1yx分别在(∞-,0),(0∞,+)内都是单调递减的,但不能说它在整个定义域,即(∞-,0)∪(0∞,+)内单调递减,只能分开写,即函数的单调减区间为(∞-,0)和(0∞,+).学.科3.函数单调性的常用结论(1)若,fxgx均为区间A上的增(减)函数,则fxgx也是区间A上的增(减)函数;(2)若0k,则kfx与fx的单调性相同;若0k,则kfx与fx的单调性相反;(3)函数0yfxfx在公共定义域内与yfx,1()yfx的单调性相反;(4)函数0yfxfx在公共定义域内与()yfx的单调性相同;(5)奇函数在其关于原点对称的区间上单调性相同,偶函数在其关于原点对称的区间上单调性相反;(6)一些重要函数的单调性:①1yxx的单调性:在,1和1,上单调递增,在1,0和0,1上单调递减;②byaxx(0a,0b)的单调性:在,ba和,ba上单调递增,在,0ba和0,ba上单调递减.4.函数的最值前提设函数yfx的定义域为,如果存在实数M满足条件(1)对于任意的xI,都有fxM;(2)存在0xI,使得0fxM(3)对于任意的xI,都有fxM;(4)存在0xI,使得0fxM结论M为最大值M为最小值注意:(1)函数的值域一定存在,而函数的最值不一定存在;(2)若函数的最值存在,则一定是值域中的元素;若函数的值域是开区间,则函数无最值,若函数的值域是闭区间,则闭区间的端点值就是函数的最值.二、函数的奇偶性1.函数奇偶性的定义及图象特点奇偶性定义图象特点偶函数如果对于函数fx的定义域内任意一个,都有fxfx,那么函数fx是偶函数图象关于y轴对称奇函数如果对于函数fx的定义域内任意一个,都有fxfx,那么函数fx是奇函数图象关于原点对称判断()fx与fx的关系时,也可以使用如下结论:如果0()fxfx或()1(()0)()fxfxfx,则函数fx为偶函数;如果0()fxfx或()1(()0)()fxfxfx,则函数fx为奇函数.注意:由函数奇偶性的定义可知,函数具有奇偶性的一个前提条件是:对于定义域内的任意一个x,x也在定义域内(即定义域关于原点对称).2.函数奇偶性的几个重要结论(1)奇函数在关于原点对称的区间上的单调性相同,偶函数在关于原点对称的区间上的单调性相反.(2)()fx,()gx在它们的公共定义域上有下面的结论:()fx()gx()()fxgx()()fxgx()()fxgx(())fgx偶函数偶函数偶函数偶函数偶函...