2025年天津市大学数学竞赛经济管理类

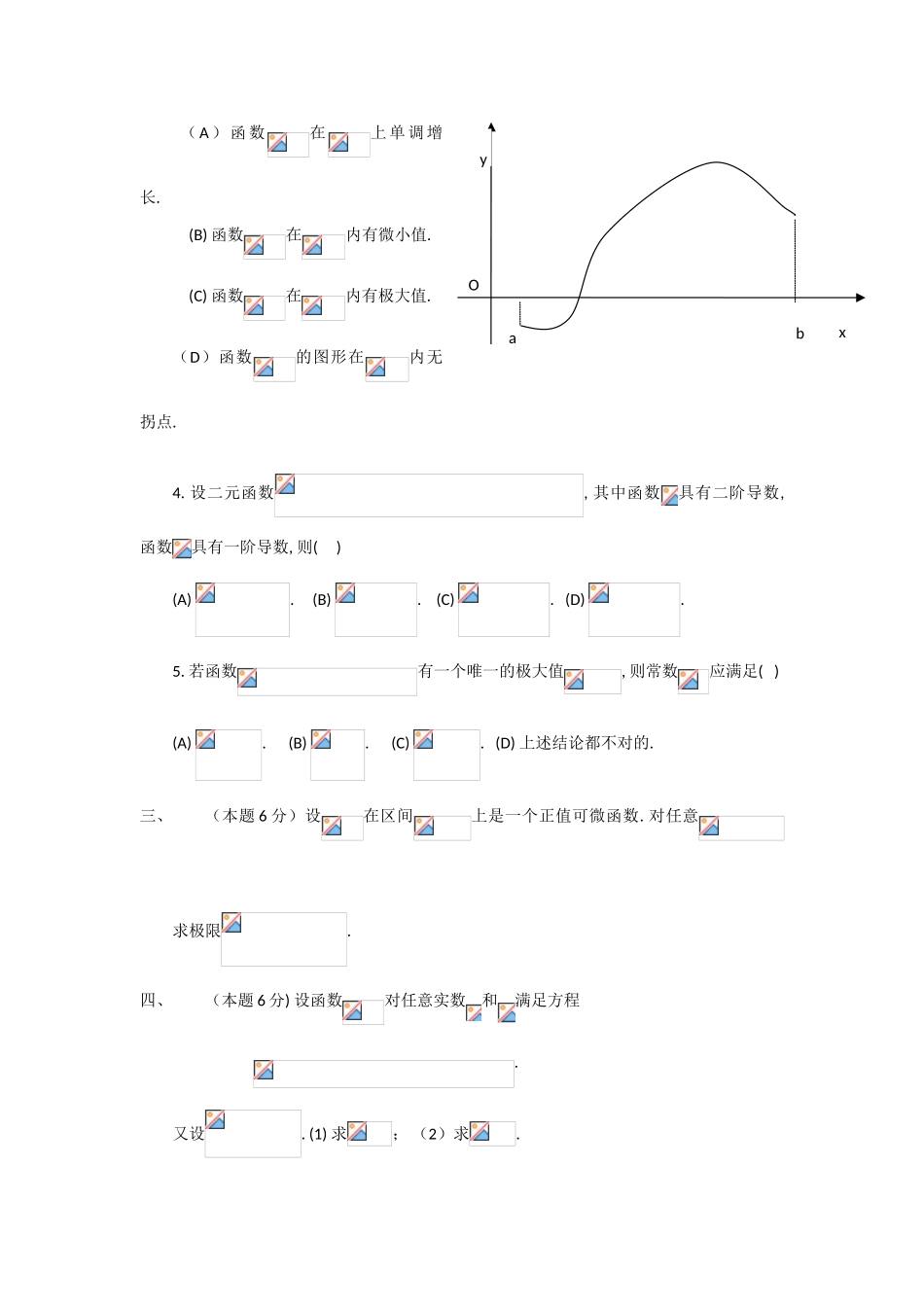
一、填空1. =_________________________.2. 设函数在的某领域内具有一阶连续导数. 若, 则=________________.3. 设函数, 是的反函数，则=__________.4. 设 函 数在 区 间上 连 续 且 单 调 增 长 ，. 若，则=____________________.5. 设, 则=______________________.二、选择1.设函数在处连续， 下列结论错误的是（ ）（A）若存在，则. (B) 若存在，则.(C) 若存在，则存在. (D) 若存在，则存在.2. 若函数可微且，则=（ ）（A）. (B) 1. (C) . (D) 2.3. 设函数在区间上连续，其图形如下图所示. 若，则（ ）Oyxba（ A ） 函 数在上 单 调 增长.(B) 函数在内有微小值.(C) 函数在内有极大值.（D）函数的图形在内无拐点.4. 设二元函数, 其中函数具有二阶导数, 函数具有一阶导数, 则( )(A) . (B) . (C) . (D) . 5. 若函数有一个唯一的极大值, 则常数应满足( )(A) . (B) . (C) . (D) 上述结论都不对的.三、（本题 6 分）设在区间上是一个正值可微函数. 对任意求极限.四、（本题 6 分) 设函数对任意实数和满足方程 . 又设. (1) 求； （2）求.五、（本题 6 分）求.六、（本题 7 分）设和都为正数. 证明：两个数和不也许同时都大于.七、（本题 7 分）设函数在区间上可导，且满足 .证明：至少存在一点，使得.八、（本题 7 分）设函数，其中 为参数. 对任意的，记为函数在闭区间上的最小值，求的表达式.九、（本题 7 分）设，其中具有二阶连续偏导数，二阶可导，求及.十、（本题 8 分）计算（1）； （2）二重积分，其中.十一、（本题 8 分）一变压器的铁心截面为对称正十字形（如图所示，在第一象限内，). 设十字形外接圆的半径为，边长所张的圆心角为（2）. 问当为什么值时，该十字形铁心截面的面积最大？并求其最大面积. 十二、（本题 8 分）如图，一只山羊被一条长为的绳子拴在半径为的圆形水池边上的点处，水池被草地围绕着. 因水池被栅栏所围，山羊不能穿越水池，但绳子可围绕在栅栏上，使山羊到达尽也许的远处（注意：在第一象限内，山羊可吃到草的区域是由点为中心为半径的上半圆，曲线及轴围成. 上的任意点满足条件：过点作圆的切线，若切点为，则的长等于圆弧的长.) 求山羊可吃到草的草地面积. OBAECDR