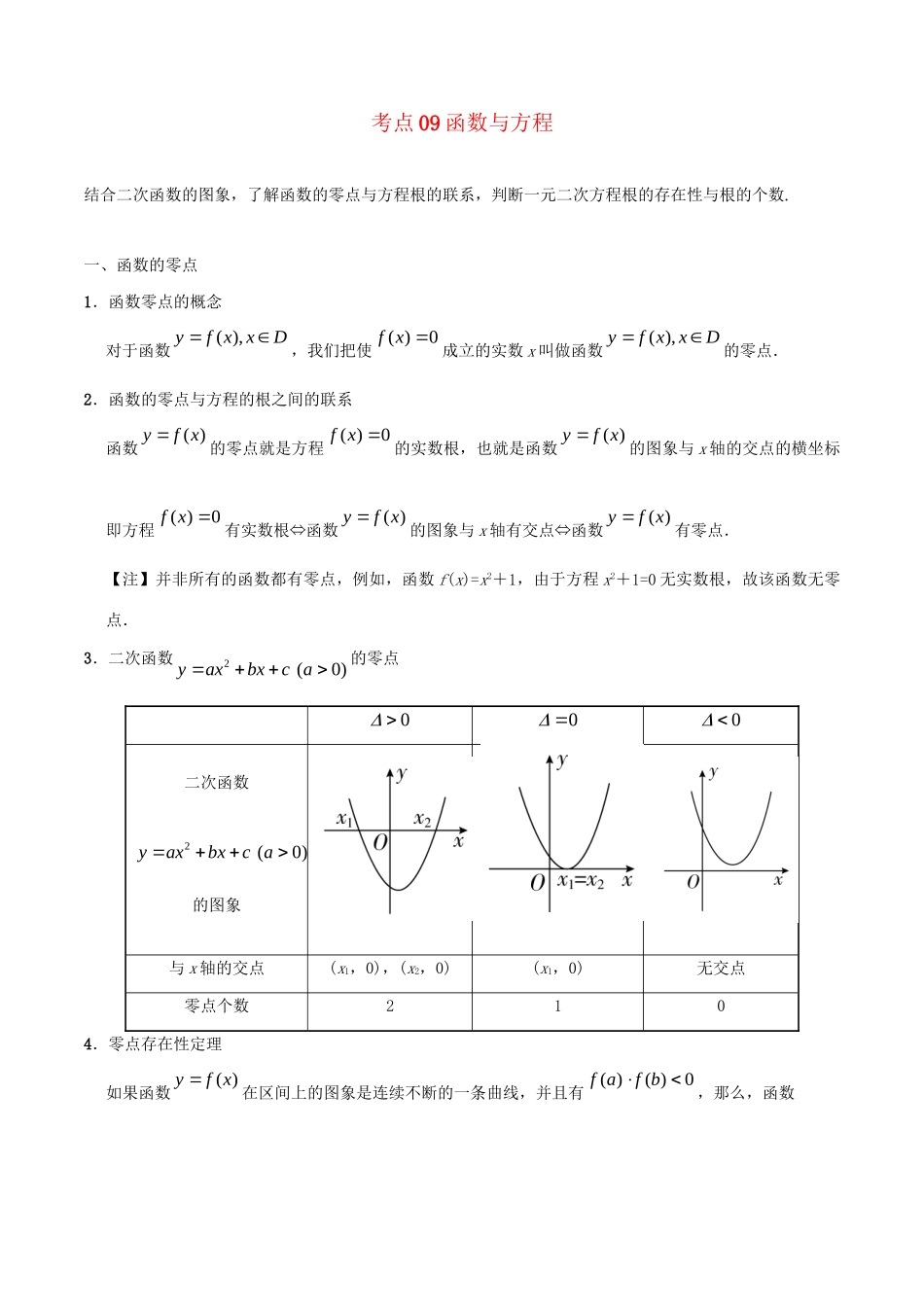
考点09函数与方程结合二次函数的图象,了解函数的零点与方程根的联系,判断一元二次方程根的存在性与根的个数.一、函数的零点1.函数零点的概念对于函数(),yfxxD,我们把使()0fx成立的实数x叫做函数(),yfxxD的零点.2.函数的零点与方程的根之间的联系函数()yfx的零点就是方程()0fx的实数根,也就是函数()yfx的图象与x轴的交点的横坐标即方程()0fx有实数根⇔函数()yfx的图象与x轴有交点⇔函数()yfx有零点.【注】并非所有的函数都有零点,例如,函数f(x)=x2+1,由于方程x2+1=0无实数根,故该函数无零点.3.二次函数2)(0yaxbxca的零点000二次函数2)(0yaxbxca的图象与x轴的交点(x1,0),(x2,0)(x1,0)无交点零点个数2104.零点存在性定理如果函数()yfx在区间上的图象是连续不断的一条曲线,并且有()()0fafb,那么,函数()yfx在区间(,)ab内有零点,即存在c∈(a,b),使得()0fc,这个也就是方程()0fx的根.【注】上述定理只能判断出零点存在,不能确定零点个数.5.常用结论(1)若连续不断的函数()fx是定义域上的单调函数,则()fx至多有一个零点;(2)连续不断的函数,其相邻两个零点之间的所有函数值保持同号;(3)函数()()()Fxfxgx有零点方程()0Fx有实数根函数()yfx与()ygx的图象有交点;(4)函数()()Fxfxa有零点方程()0Fx有实数根函数()yfx与ya的图象有交点{|()}ayyfx,其中为常数.二、二分法1.二分法的概念对于在区间上连续不断且()()0fafb的函数()yfx,通过不断地把函数()fx的零点所在的区间一分为二,使区间的两个端点逐步逼近零点,进而得到零点近似值的方法叫做二分法.2.用二分法求函数()fx零点近似值的步骤给定精确度ε,用二分法求函数()fx零点近似值的步骤如下:①确定区间,验证()()0fafb,给定精确度ε;②求区间(a,b)的中点c;③计算f(c);a.若f(c)=0,则c就是函数的零点;b.若f(a)·f(c)<0,则令b=c(此时零点x0∈(a,c));c.若f(c)·f(b)<0,则令a=c(此时零点x0∈(c,b)).④判断是否达到精确度ε:即若|a−b|<ε,则得到零点近似值a(或b);否则重复②③④.【速记口诀】定区间,找中点;中值计算两边看,同号丢,异号算,零点落在异号间.重复做,何时止,精确度来把关口.考向一函数零点(方程的根)所在区间的判断函数零点的判定方法(1)定义法(定理法):使用零点存在性定理,函数()yfx必须在区间上是连续的,当()()fafb0时,函数在区间(a,b)内至少有一个零点.(2)方程法:判断方程()0fx是否有实数解.(3)图象法:若一个函数(或方程)由两个初等函数的和(或差)构成,则可考虑用图象法求解,如()()()fxgxhx,作出()ygx和()yhx的图象,其交点的横坐标即为函数f(x)的零点.典例1函数21()ln1fxxx的零点所在的大致区间是A.(1,2)B.(2,3)C.(3,4)D.(1,2)与(2,3)【答案】B【规律总结】判断函数零点所在区间的方法:一般而言判断函数零点所在区间的方法是将区间端点代入函数求出函数的值,进行符号判断即可得出结论.此类问题的难点往往是函数值符号的判断,可运用函数的有关性质进行判断.1.方程log3x+x=3的解所在的区间为A.(0,2)B.(1,2)C.(2,3)D.(3,4)考向二函数零点个数的判断判断函数零点个数的方法(1)解方程法:令f(x)=0,如果能求出解,则有几个解就有几个零点.学%(2)零点存在性定理法:利用定理不仅要求函数在区间上是连续不断的曲线,且f(a)·f(b)<0,还必须结合函数的图象与性质(如单调性、奇偶性、周期性、对称性)才能确定函数有多少个零点或零点值所具有的性质.(3)数形结合法:转化为两个函数的图象的交点个数问题,先画出两个函数的图象,看其交点个数,其中交点的横坐标有几个不同的值,就有几个不同的零点.典例2函数f(x)=2x+lg(x+1)2−的零点有A.0个B.1个C.2个D.3个【答案】B解法二:在同一坐标系中作出h(x)=22−x和g(x)=lg(x+1)的图象,如图所示,由图象可知h(x)=22−x和g(x)=lg(x+1)有且只有一个交点,即f(x)=2x+lg(x+1)2−与x轴有且只有一个交点,即函数f(x)仅有一个零点.2.函数223,0()=2ln,...