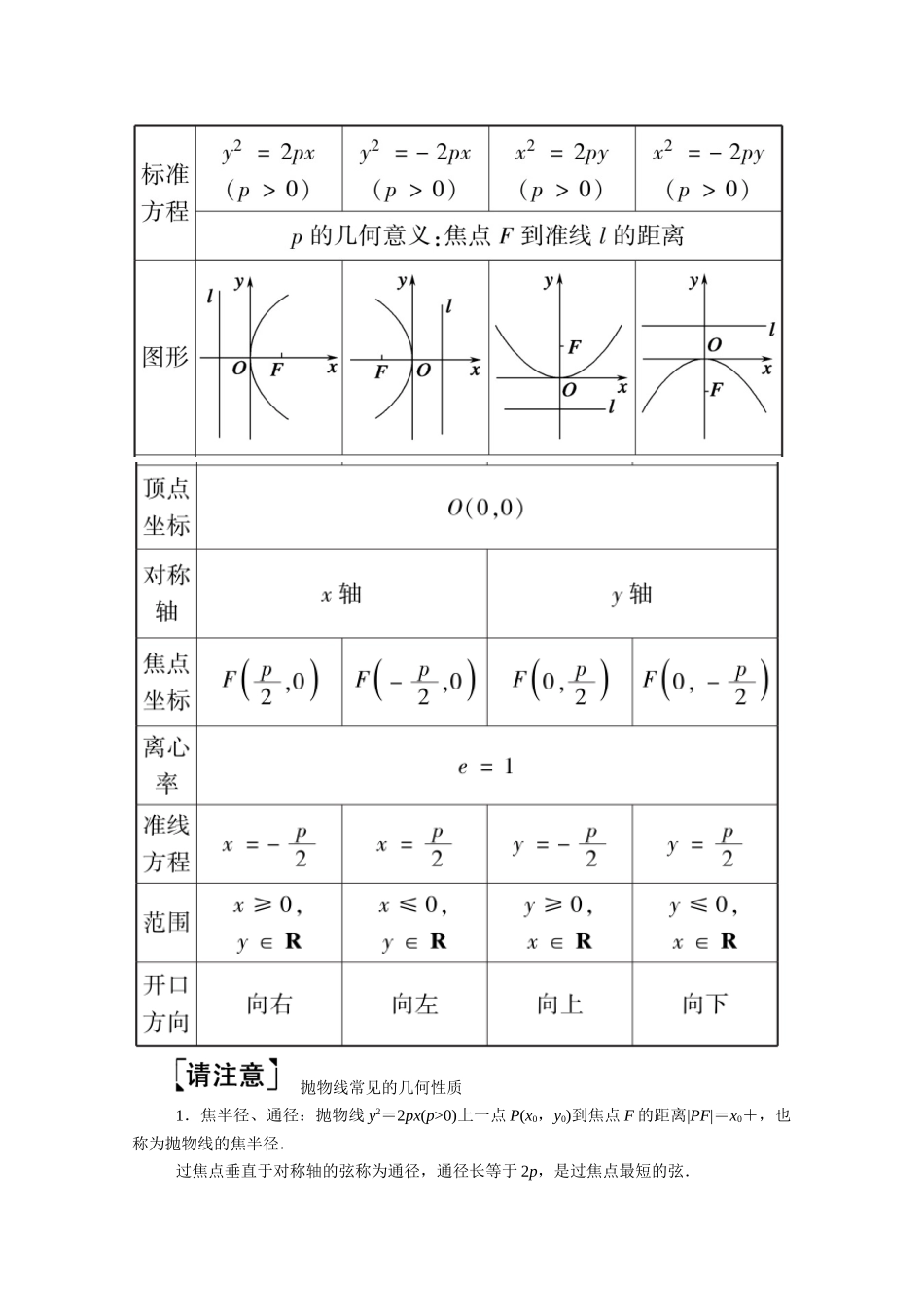
第七节 抛物线课标要求考情分析1.掌握抛物线的定义、几何图形、标准方程及简单几何性质(范围、对称性、顶点、离心率).2.理解数形结合的思想.3.了解抛物线的实际背景及抛物线的简单应用.1.抛物线的定义、标准方程、几何性质是近几年高考命题方向方向的热点.2.常与圆、椭圆、双曲线、直线、导数等知识交汇命题方向方向.3.题型主要以解答题的形式出现,属于中高档题,有时也会以选择题、填空题的形式出现,属中低档题. 知识点一 抛物线的定义平面内与一个定点 F 和一条定直线 l(l 不经过点 F)距离相等的点的轨迹叫做抛物线.点F 叫做抛物线的焦点,直线 l 叫做抛物线的准线.数学表达式:| MF | = d ( 其中 d 为点 M 到准线的距离 ) .当定点在定直线上时,轨迹为过定点 F 与定直线 l 垂直的一条直线.知识点二 抛物线的标准方程及几何性质抛物线常见的几何性质1.焦半径、通径:抛物线 y2=2px(p>0)上一点 P(x0,y0)到焦点 F 的距离|PF|=x0+,也称为抛物线的焦半径.过焦点垂直于对称轴的弦称为通径,通径长等于 2p,是过焦点最短的弦.2.直线 AB 过抛物线 y2=2px(p>0)的焦点,交抛物线于 A(x1,y1),B(x2,y2)两点,如图可得.①y1y2=-p2,x1x2=.②|AB|=x1+x2+p,x1+x2≥2=p,即当 x1=x2时,弦长最短为 2p.③+为定值.④ 弦长 AB=(α 为 AB 的倾斜角).⑤ 以 AB 为直径的圆与准线相切.⑥ 焦点 F 对 A,B 在准线上射影的张角为 90°.1.思考辨析判断下列结论正误(在括号内打“√”或“×”)(1)平面内与一个定点 F 和一条定直线 l 的距离相等的点的轨迹一定是抛物线.( × )(2)抛物线 y2=4x 的焦点到准线的距离是 4.( × )(3)若一抛物线过点 P(-2,3),其标准方程可写为 y2=2px(p>0).( × )2.小题热身(1)以 x=1 为准线的抛物线的标准方程为( D )A.y2=2x B.y2=-2xC.y2=4x D.y2=-4x(2)设抛物线 y2=2px(p>0)的焦点在直线 2x+3y-8=0 上,则该抛物线的准线方程为( D )A.x=-1 B.x=-2C.x=-3 D.x=-4(3)已知点 F,直线 l:x=-,点 B 是 l 上的动点.若过点 B 垂直于 y 轴的直线与线段BF 的垂直平分线交于点 M,则点 M 的轨迹是( D )A.双曲线 B.椭圆C.圆 D.抛物线(4)抛物线 8x2+y=0 的焦点坐标为.(5)若抛物线 y=4x2上的一点 M 到焦点的距离为 1,则点 M 的纵坐标是.解析:(2)因...