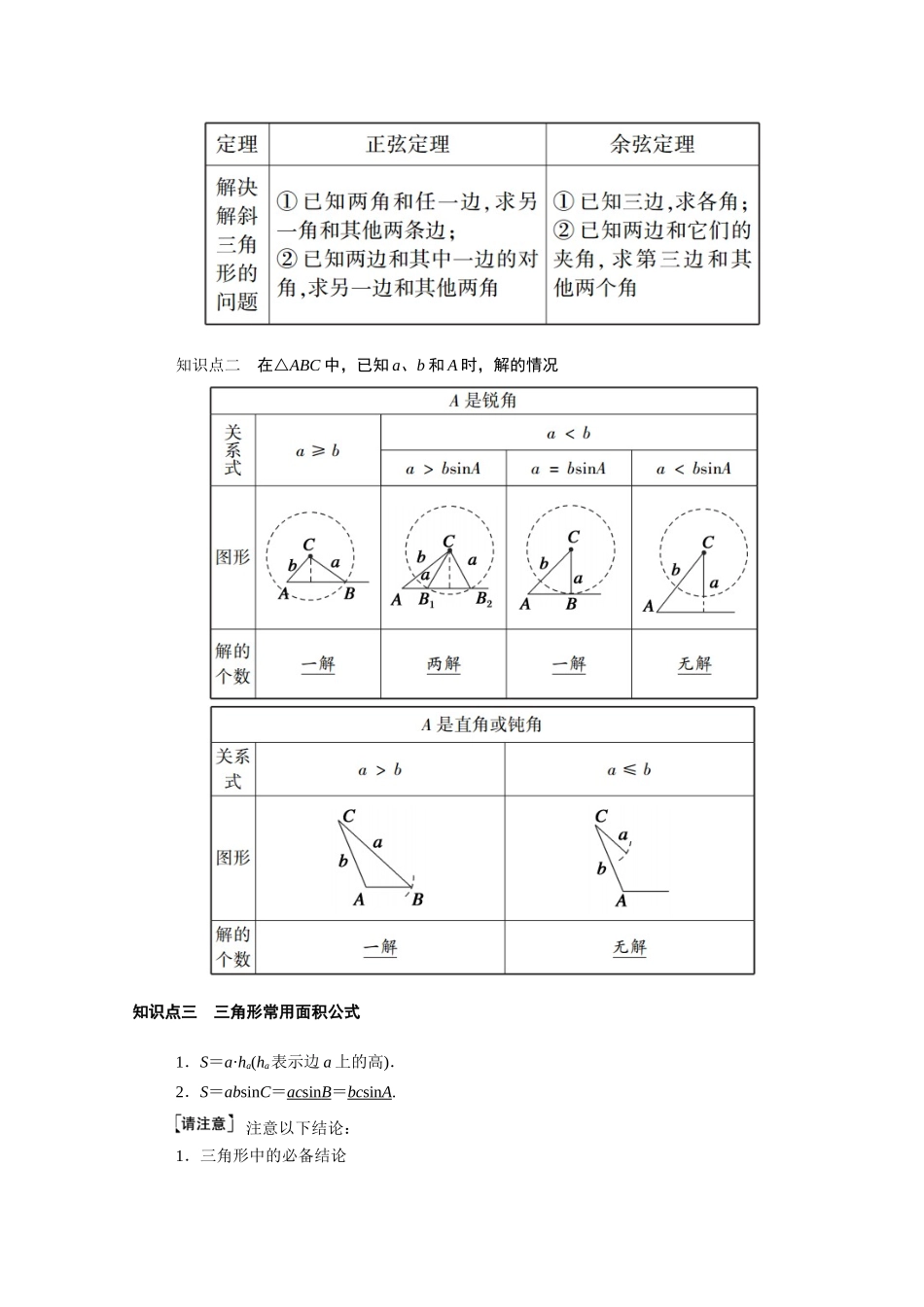
第六节 正弦定理和余弦定理课标要求考情分析掌握正弦定理、余弦定理,并能解决一些简单的三角形度量问题.1.本节是高考中的重点考查内容,主要考查利用正、余弦定理解三角形、判断三角形的形状,求三角形的面积等.2.命题形式多种多样,解答题以综合题为主,常与三角恒等变换、平面向量相结合. 知识点一 正弦定理和余弦定理知识点二 在△ABC 中,已知 a、b 和 A 时,解的情况知识点三 三角形常用面积公式1.S=a·ha(ha表示边 a 上的高).2.S=absinC=ac sin B =bc sin A .注意以下结论:1.三角形中的必备结论(1)a>b⇔A>B(大边对大角).(2)A+B+C=π(三角形内角和定理).(3)sin(A+B)=sinC,cos(A+B)=-cosC,sin=cos,cos=sin.(4)射影定理:bcosC+ccosB=a,bcosA+acosB=c,acosC+ccosA=b.2.利用正、余弦定理解三角形时,要注意三角形内角和定理对角的范围的限制.1.思考辨析判断下列结论正误(在括号内打“√”或“×”)(1)三角形中三边之比等于相应的三个内角之比.( × )(2)当 b2+c2-a2>0 时,三角形 ABC 为锐角三角形.( × )(3)在△ABC 中,=.( √ )(4)在三角形中,已知两边和一角就能求三角形的面积.( √ )2.小题热身(1)在锐角△ABC 中,角 A,B 所对的边长分别为 a,b,2asinB=b,则角 A 等于( C )A. B.C. D.(2)已知锐角△ABC 的面积为 3,BC=4,CA=3,则角 C 的大小为( B )A.75° B.60°C.45° D.30°(3)在△ABC 中,已知 b=40,c=20,C=60°,则此三角形的解的情况是( C )A.有一解 B.有两解C.无解 D.有解但解的个数不确定(4)在△ABC 中,A=60°,AC=4,BC=2,则△ABC 的面积等于 2.(5)在△ABC 中,sin2A≤sin2B+sin2C-sinBsinC,则 A 的取值范围是.解析:(1)由 2asinB=b 可得:2sinAsinB=sinB,故 sinA=,A=.(2)由三角形的面积公式,得 BC·CA·sinC=3,即×4×3sinC=3,解得 sinC=,又因为三角形为锐角三角形,所以 C=60°.(3)由三角形正弦定理=,即=,解得 sinB=,B 无解,所以三角形无解.故本题正确答案为 C.(4)设△ABC 中,角 A,B,C 对应的边分别为 a,b,c.由题意及余弦定理得 cosA===,解得 c=2.所以 S=bcsinA=×4×2×sin60°=2.(5)由已知不等式结合正弦定理得 a2≤b2+c2-bc,所以 b2+c2-a2≥bc,所以 cosA=≥.因为 y=cosx 在上为减函数.故 A 的取值范围是.第 1 课...