皮尔逊Ⅲ型曲线VIP专享

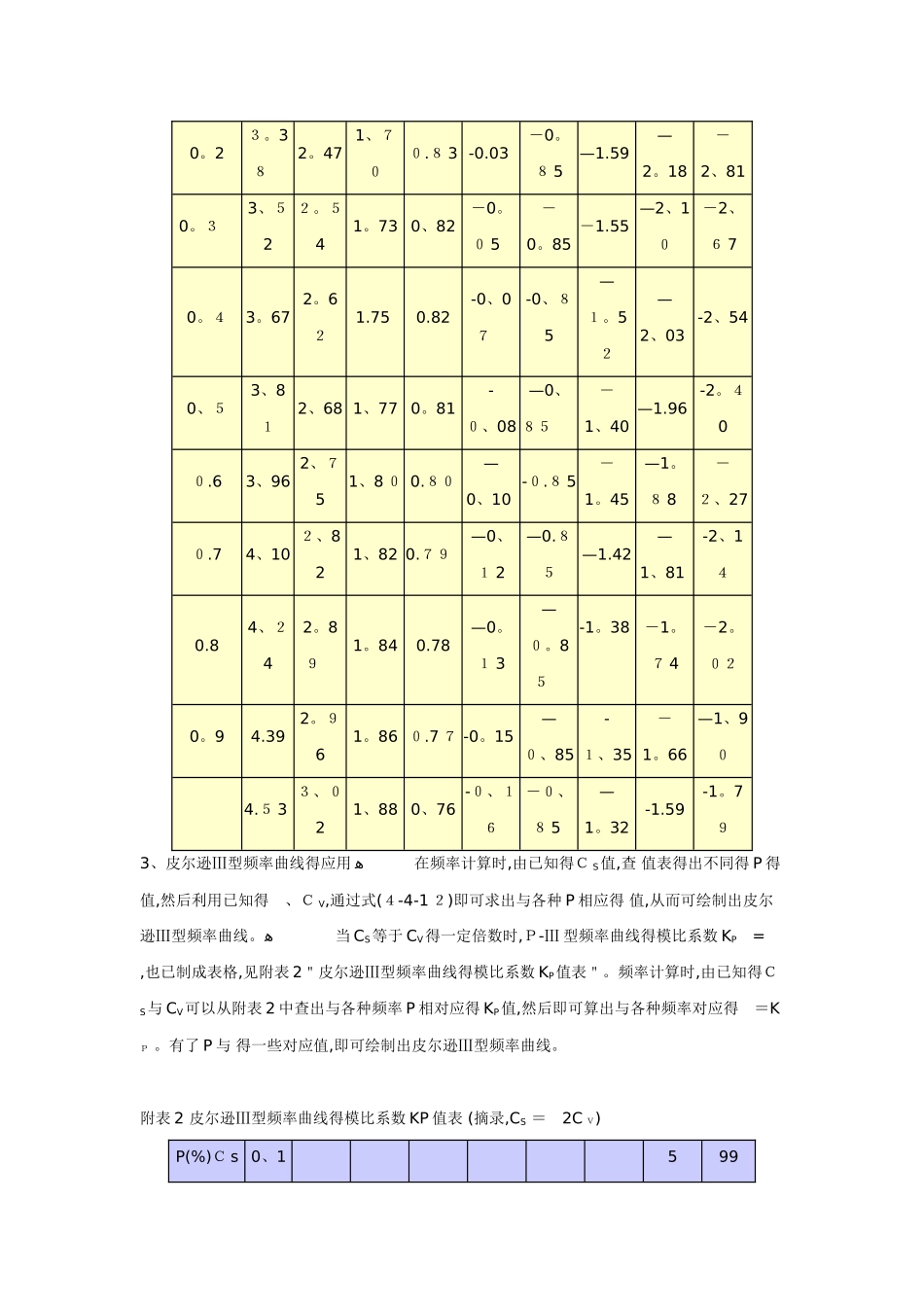
皮尔逊Ⅲ(P-Ⅲ)型曲线１、皮尔逊Ⅲ型曲线得概率密度函数ﻫ 皮尔逊Ⅲ型曲线就是一条一端有限一端无限得不对称单峰、正偏曲线(见图 4－4-3),数学上常称伽玛分布,其概率密度函数为: (4-4—８) ﻫ 式中:Γ(α)―α 得伽玛函数; α、β、a ０―分别为皮尔逊Ⅲ型分布得形状尺度与位置未知参数,ﻫ α0, β0 ﹥﹥。显然,三个参数确定以后,该密度函数随之可以确定。可以推论,这三个参数与总体三个参数 、Ｃｖ、CS 具有如下关系:ﻫ (4—４-9) 2、皮尔逊Ⅲ型频率曲线及其绘制 水文计算中,一般需要求出指定频率 P 所相应得随机变量取值 xp,也就就是通过对密度曲线进行积分,即:ﻫ (4-4-10) 求出等于及大于 xp 得累积频率 P 值。直接由式(4—４-10)计算 P 值非常麻烦,实际做法就是通过变量转换,变换成下面得积分形式 :ﻫﻫ ( ４－4-１1)ﻫ 式(4-4-11)中被积函数只含有一个待定参数 C Ｓ,其它两个参数 、Cv 都包含在 中、 ,ｘ就是标准化变量,称为离均系数。 得均值为 0,标准差为 1、因此,只需要假定一个Ｃ S 值,便可从式(4-4—１１)通过积分求出 与 之间得关系、对于若干个给定得Ｃ S值, 得对应数值表,已先后由美国福斯特与前苏联雷布京制作出来,见附表１"皮尔逊Ⅲ型频率曲线得离均系数 值表”。由 就可以求出相应频率 得 x 值: ﻫﻫ ( 4－４－12)ﻫ附表 1 皮尔逊Ⅲ型频率曲线得离均系数 值表(摘录) P(％)Cs 0.1１52 ０50 809 ５ 99 99、90。0３。０92、33 1。64 ０。84 0.0 ０ -０。84—１、６ 4-2。３3-３、０９0。13、23 1、67 2、0 0、84 -０。０2 -０.85 -1.62 -2。２5—2.９50。2３。3８ 2。471、７００.８ 3 -0.03 －0。８ 5—1.59 —2。18－2、810。３ 3、５2２。５41。730、82－0。０ 5 －0。85－1.55 —2、1０－2、６ 70。４3。672。6２1.75 0.82-0、0７ -0、８5—１。5２—2、03 -2、540、５3、8１2、68 1、770。81-０、08—0、８５ －1、40—1.96 -2。４0０.63、962、７51、8 ０ 0.８０—0、10 -０.８ 5－1。45—1。８ 8 －２、27０.74、10２、821、82 0.７９ —0、１ 2—0.８５—1.42—1、81 -2、1４0.84、２42。8９ 1。840.78—0。１ 3—０。8５ -1。38 －1。７ 4－2。０２0。94.392。９61。86 ０.7 ７ -0。15 —０、85-１、35－1。66—1、9０ 4.５ 3 ３、０21、880、76-０、１６－０、８ 5 —1。32-1.59-1。7９3、皮尔逊...