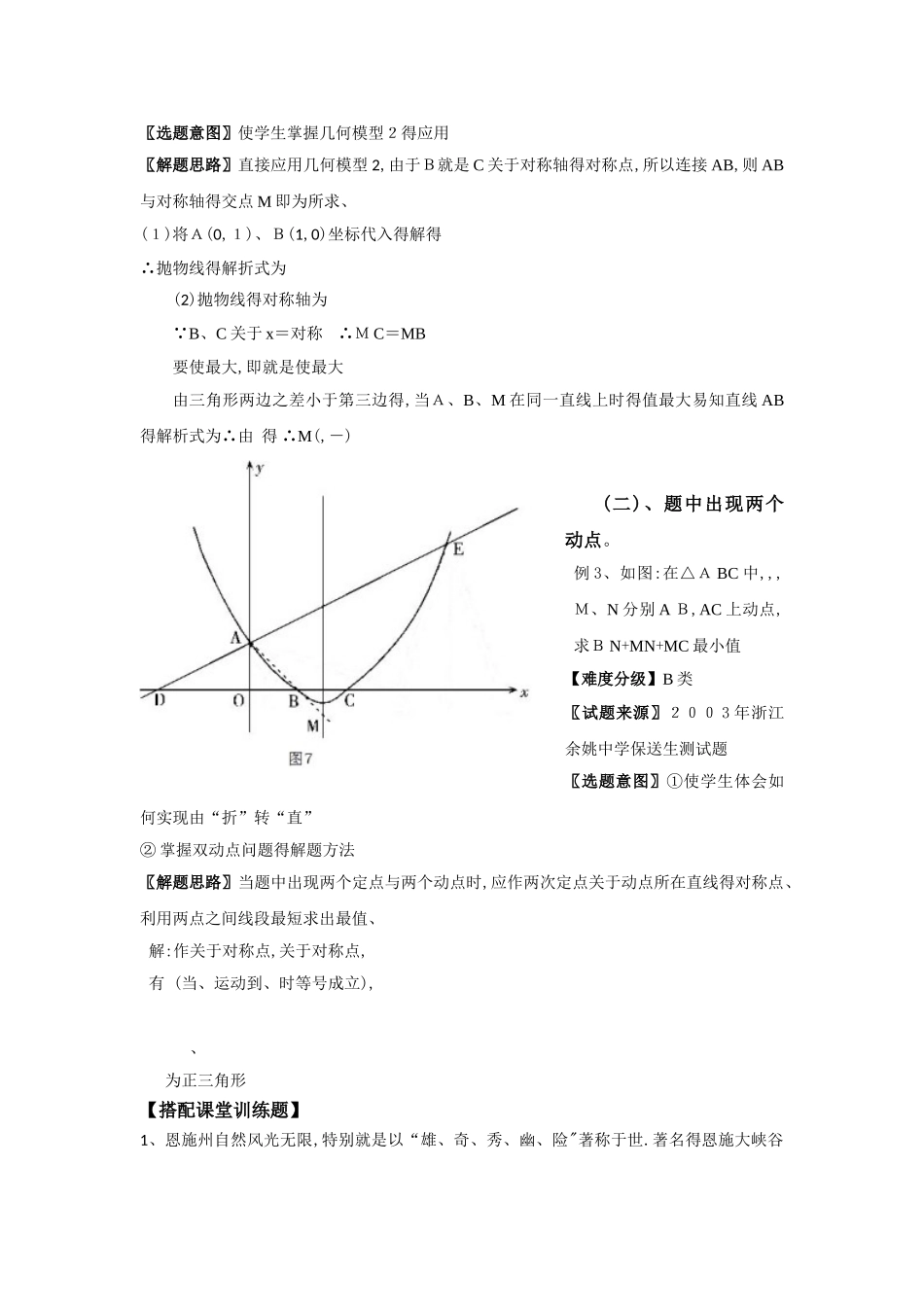
第三讲 最短距离问题一、知识梳理几何模型 1条件:如图,、就是直线同旁得两个定点。问题:在直线上确定一点,使得值最小。方法:作点关于直线得对称点,连结交于点,则得值最小几何模型 2条件:如图,、就是直线异侧得两个定点.且 A、B 到距离不相等问题:在直线上确定一点,使得值最大方法:作点关于直线得对称点,连结交于点,则得值最小二、方法归纳对于几何模型 1,近年来,除了常见得“一个动点”外,出现了“两个动点”、 “三个动点" 等变式问题得问题,而解决此类问题得关键在于:找点关于线得对称点,实现“折”转“直”。对于几何模型 2,近年出现得中考题都就是直接应用。三、课堂精讲例题 (一)、题中出现一个动点。例 1、在正方形A BCD 中,点 E 为 BC 上一定点,且BE=1 0,CE=14,P为 BD 上一动点,求 P E+P C最小值。【难度分级】A 类〖试题来源〗经典例题〖选题意图〗使学生掌握几何模型 1 得应用〖解题思路〗作关于对称点,可以证明在上,易求解:作关于对称点 四边形 ABC D就是正方形 在上,且 即就是得最小值 【搭配课堂训练题】1、已知:抛物线得对称轴为 x=—1 与轴交于两点,与轴交于点其中、(1)求这条抛物线得函数表达式.(2)已知在对称轴上存在一点P,使得得周长最小、请求出点 P 得坐标【难度分级】A 类〖试题来源〗2025 年山东济南中考真题。〖答案〗解:(1)由题意得 解得∴此抛物线得解析式为(2)连结、、因为得长度一定,所以周长最小,就就是使最小。点关于对称轴得对称点就是点,与对称轴得交点即为所求得点. 设直线得表达式为则解得∴此直线得表达式为把代入得∴点得坐标为例 2:已知:直线与轴交于 A,与轴交于D,抛物线与直线交于A、E 两点,与轴交于 B、C 两点,且 B 点坐标为 (1,0).(1)求抛物线得解析式;(2)在抛物线得对称轴上找一点M,使得值最大,求出点 M 得坐标.【难度分级】A类〖试题来源〗2 0 09 眉山中考数学真题〖选题意图〗使学生掌握几何模型2得应用〖解题思路〗直接应用几何模型 2,由于B就是 C 关于对称轴得对称点,所以连接 AB,则 AB与对称轴得交点 M 即为所求、(1)将A(0,1)、B(1,0)坐标代入得解得∴抛物线得解折式为(2)抛物线得对称轴为 B、C 关于 x=对称 ∴M C=MB要使最大,即就是使最大 由三角形两边之差小于第三边得,当A、B、M 在同一直线上时得值最大易知直线 AB得解析式为∴由 得 ∴M(,-) (二)、题中出现两个动点。例 3、如图:在△A BC...