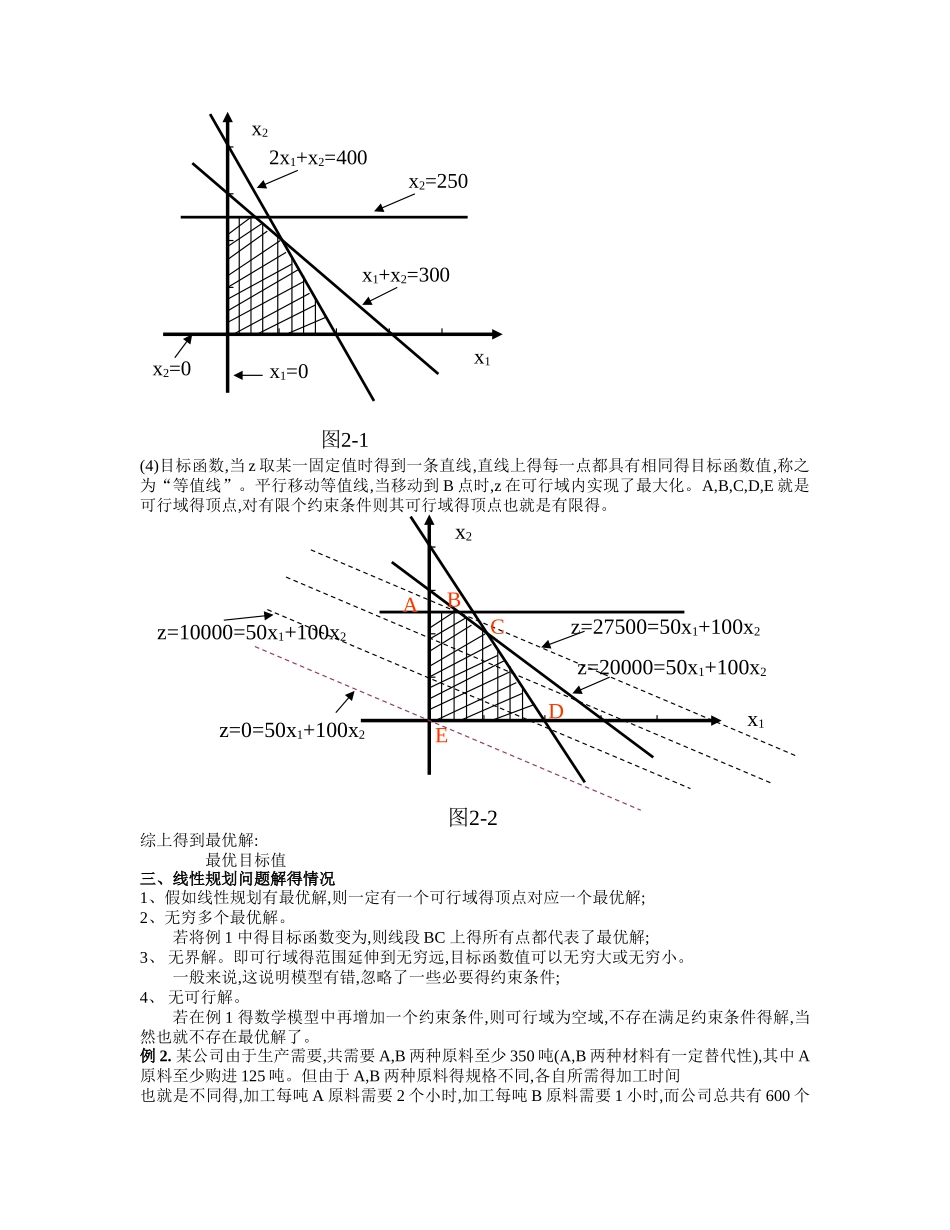
第 2 次课 2 学时 本次课教学重点: 线型规划模型有关概念、图解法求解线型规划模型本次课教学难点: 线型规划模型有关概念、各种解得情况分析本次课教学内容:第二章 线性规划得图解法第一节 问题得提出一、引例例 1、 某工厂在计划期内要安排Ⅰ、Ⅱ两种产品得生产,已知生产单位产品所需得设备台时及A、B 两种原材料得消耗、资源得限制,如下表:ⅠⅡ资源限制设备11300 台时原料 A21400 千克原料 B01250 千克单位产品获利50 元100 元问题:工厂应分别生产多少单位Ⅰ、Ⅱ产品才能使工厂获利最多?解:分析问题后可得数学模型: 目标函数: 约束条件: 这就是一个线性规划模型,因为:目标函数就是线性函数,约束条件就是一些线性得等式或不等式。若目标函数就是非线性函数,或约束条件中有非线性得等式或不等式,则这样得问题称为非线性规划。二、一般建模过程1、理解要解决得问题,了解解题得目标与条件;2、定义决策变量,每一组值表示一个方案;3、用决策变量得线性函数形式写出目标函数,确定最大化或最小化目标;4、用一组决策变量得等式或不等式表示解决问题过程中必须遵循得约束条件三、线性规划模型得一般形式目标函数: 约束条件: …… …… 第二节 图 解 法对于只有两个决策变量得线性规划问题,可以在平面直角坐标系上作图表示线性规划问题得有关概念,并求解。 下面通过例 1 详细讲解其方法一、有关概念1、 可行解:满足约束条件得解2、 可行域:全体可行解得集合。3、 最优解:使得目标函数值达到最优得可行解。4、 凸集5、 松弛变量二、图解法求解线性规划例 1、 目标函数: 约束条件: 解:(1)分别取决策变量为坐标向量建立直角坐标系。在直角坐标系里 ,图上任意一点得坐标代表了决策变量得一组值,例 1 得每个约束条件都代表一个半平面。(2)对每个不等式(约束条件),先取其等式在坐标系中作直线,然后确定不等式所决定得半平面。(3)把五个图合并成一个图,取各约束条件得公共部分,如图 2-1 所示。x2x1X2≥0X2=0x2x1X1≥0X1=0100200300100200300x1+x2≤300x1+x2=3001001002002x1+x2≤4002x1+x2=400300200300400100100x2≤250x2=250200300200300(4)目标函数,当 z 取某一固定值时得到一条直线,直线上得每一点都具有相同得目标函数值,称之为“等值线”。平行移动等值线,当移动到 B 点时,z 在可行域内实现了最大化。A,B,C,D,E 就是可行域得顶点,对有限个约束条件则其可行域得顶点也就是有限得。综上得到最优解: 最优...