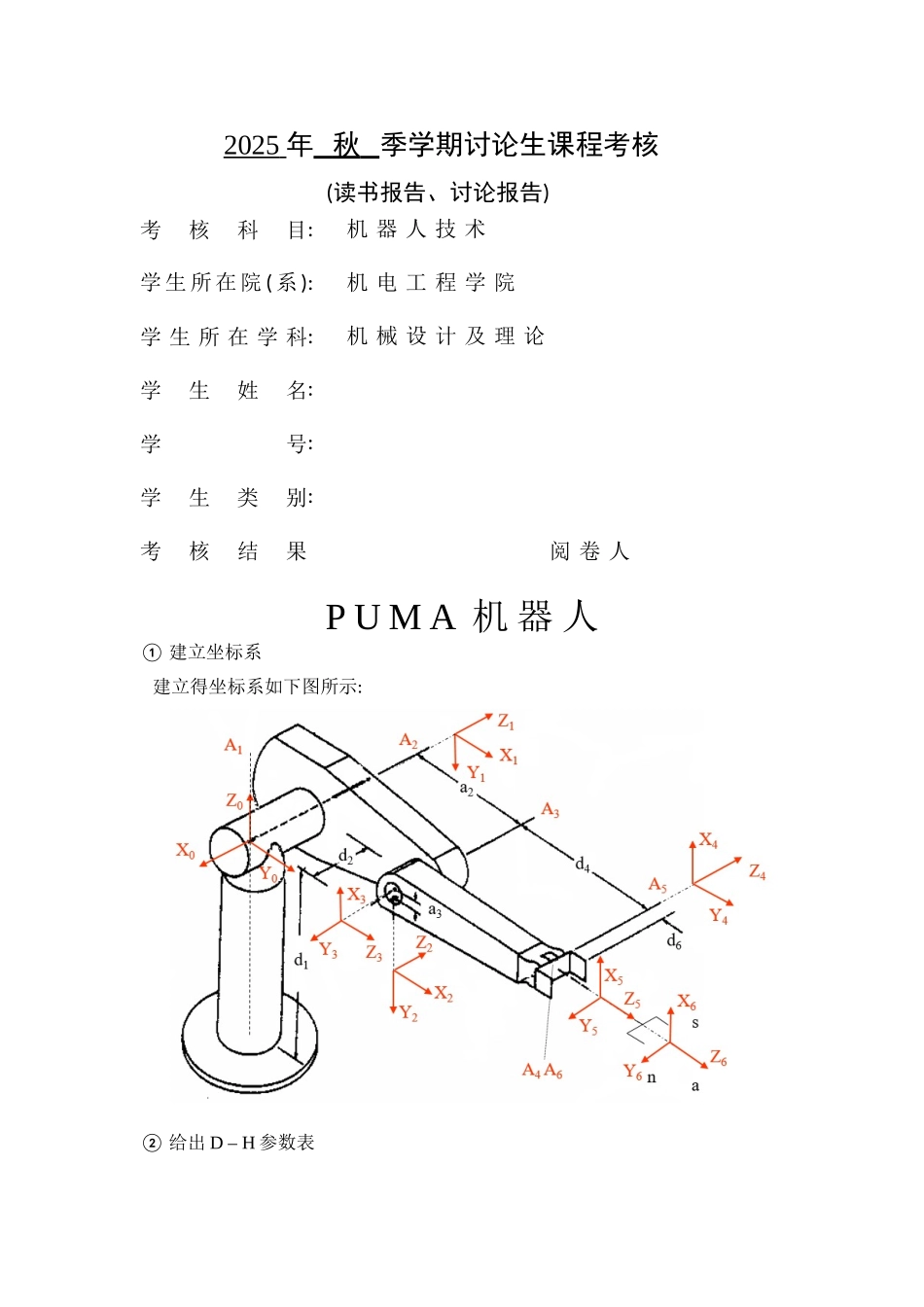
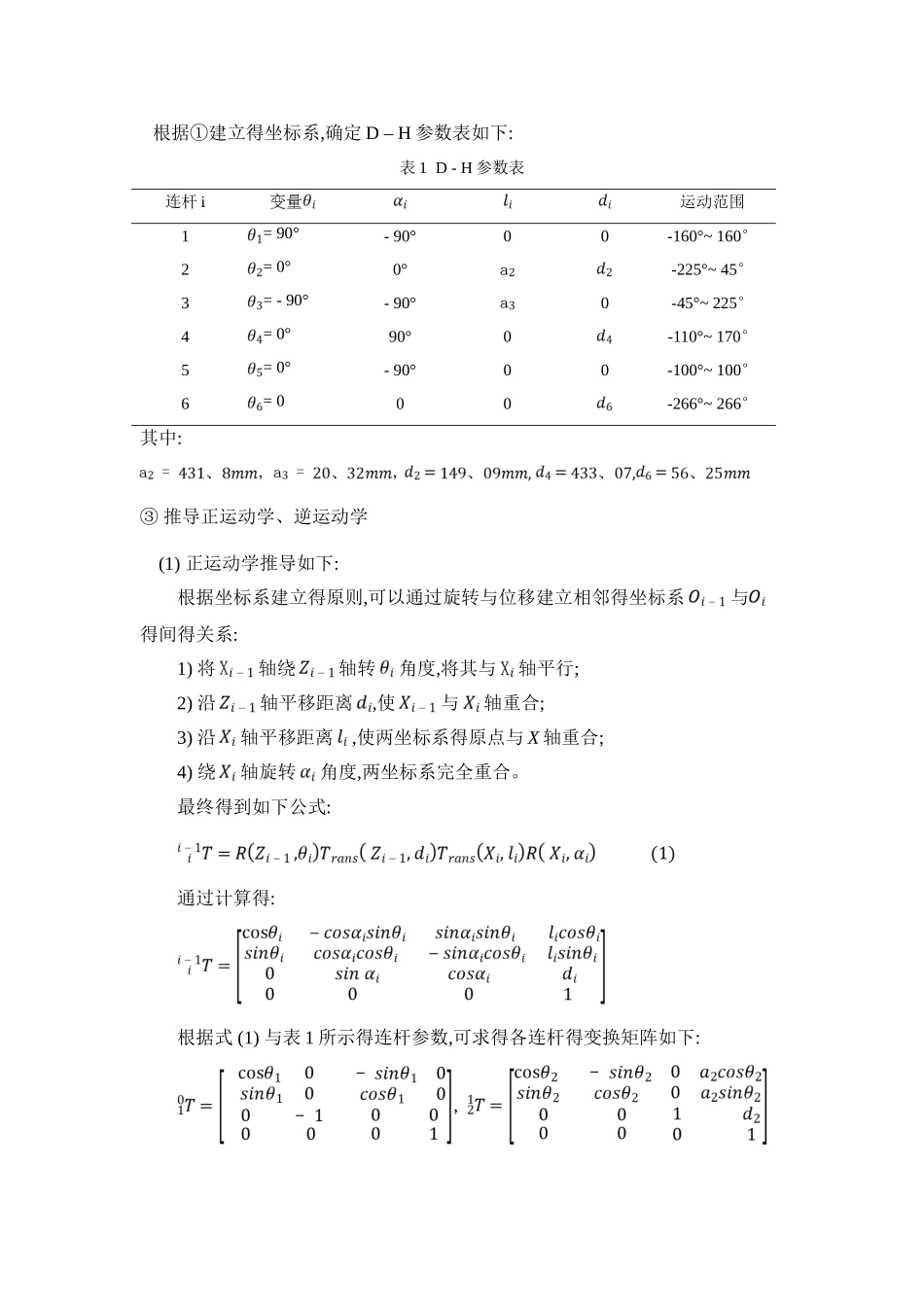
2025 年 秋 季学期讨论生课程考核(读书报告、讨论报告)考核科目: 机 器 人 技 术 学 生 所 在 院 ( 系 ): 机 电 工 程 学 院学 生 所 在 学 科: 机 械 设 计 及 理 论学 生 姓 名: 学 号: 学 生 类 别: 考核结果阅 卷 人P U M A 机 器 人① 建立坐标系 建立得坐标系如下图所示:② 给出 D – H 参数表 根据①建立得坐标系,确定 D – H 参数表如下:表 1 D - H 参数表连杆 i运动范围1= 90°- 90°00-160°~ 160°2= 0°0°-225°~ 45°3= - 90°- 90°0-45°~ 225°4= 0°90°0-110°~ 170°5= 0°- 90°00-100°~ 100°6= 000-266°~ 266°其中:③ 推导正运动学、逆运动学(1) 正运动学推导如下:根据坐标系建立得原则,可以通过旋转与位移建立相邻得坐标系与得间得关系:1) 将轴绕轴转角度,将其与轴平行;2) 沿轴平移距离,使与轴重合;3) 沿轴平移距离,使两坐标系得原点与 X 轴重合;4) 绕轴旋转角度,两坐标系完全重合。最终得到如下公式:通过计算得:根据式 (1) 与表 1 所示得连杆参数,可求得各连杆得变换矩阵如下:, , , 各连杆得变换矩阵相乘,得到该机器人得机械手变换矩阵:将求得得各连杆变换矩阵带入相乘,得到机械手得变换矩阵为:其中: (2) 逆运动学推导如下: (取)1) 求用逆变换 左乘方程 (2) 两边,即有: (4)令矩阵方程 (4) 两端得元素相等,可得:利用三角代换:式中,。把代换式 (6) 代入式 (5) 得:式中,正、负号对应于得两个可能解。2) 求矩阵方程两端得元素(1,4)与(2,4)分别对应相等平方与为:其中解得:3) 求在矩阵方程两边左乘逆变换。方程两边得元素(1,4)与(3,4)分别对应相等,得联立,得与与表达式得分母相等,且为正,于就是 根据解与得四种可能组合,可以得到相应得四种可能值,于就是可得 得四种可能解式中取与相对应得值。4) 求令两边元素(1,3)与(2,3)分别对应相等,则可得只要,便可求出当时,机械手处于奇异形位。5) 求根据矩阵两边元素(1,3)与(2,3)分别对应相等,可得6) 求根据矩阵两边元素(2,1)与(1,1)分别对应相等,可得 从而求得④ 用 Matlab 编程得出工作空间工作空间:机器人得手臂或手部安装点所能到达得所有空间区域,不包括手部本身所能到达得空间区域。可将第 5 个坐标系得坐标原点瞧作手部安装点,计算工作空间时,将第 5 个坐标系得坐标原点当作动点,取将其带入步骤②计算出表达式,即可求得动点得位置(工作空...