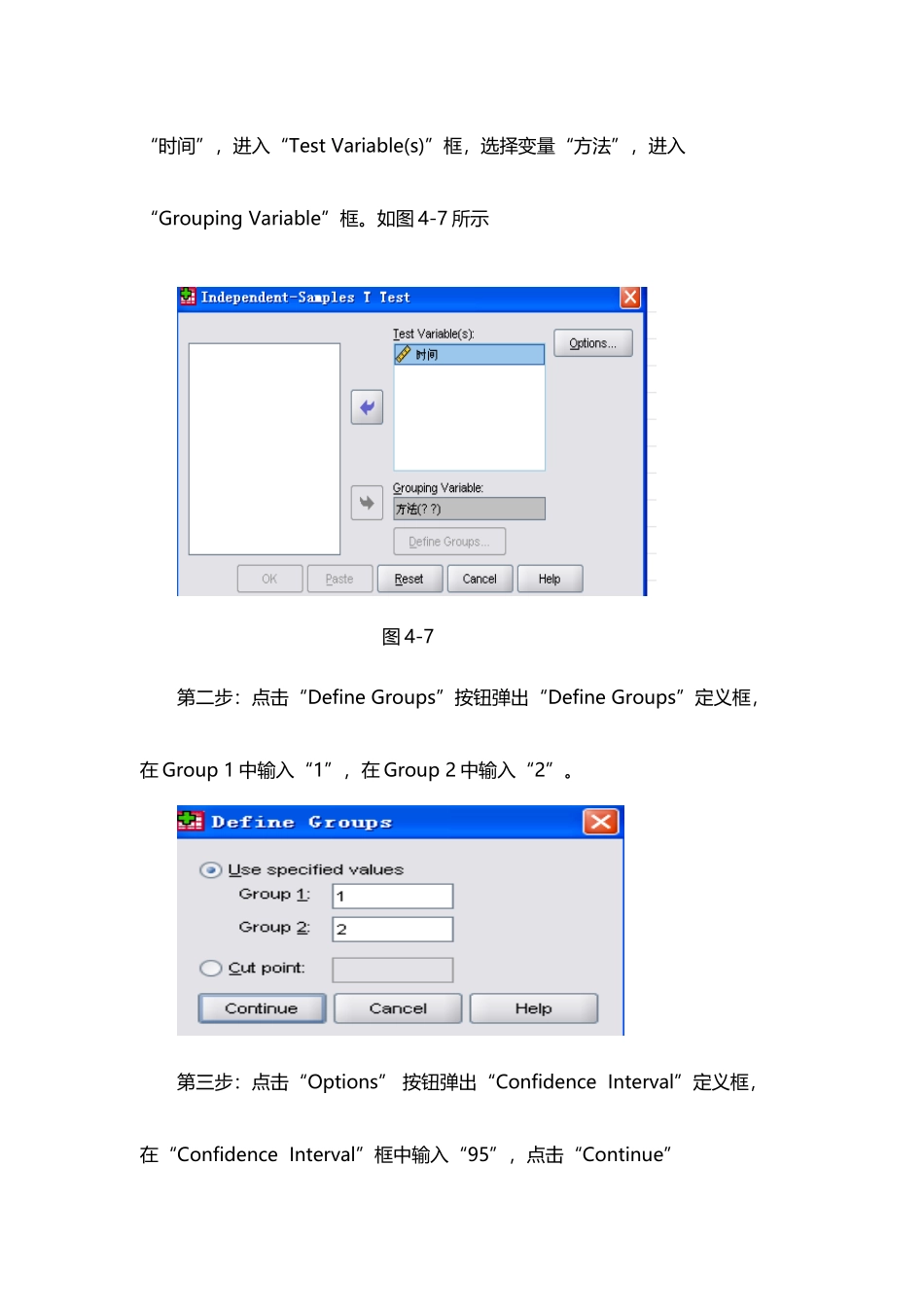
两个正态总体均值差的区间估量(5 页)Good is good, but better carries it
精益求精，善益求善
两个正态总体均值差的区间估量实验一一、实验目的熟悉的参数估量功能，熟练掌握两个正态总体均值之差（独立样本）的区间估量方法及操作过程，对运行结果能进行解释
二、实验内容【例】（数据文件为data03-1
sav）为估量两种方法组装产品所需要时间的差异，分别对两种不同的组装方法个随机安排12个工人，每个工人组装一件产品所需的时间（分钟）
数据如表1所示：表 1 两种方法组装产品所需的时间方法1方法2方法1方法228
5试以95%的置信水平确定两种方法组装产品所需时间差值的置信区间
解：第一步，打开数据文件“data03-1
sav”，选择菜单“Analyze→Compare Means→Independent-samples T Test”项，弹出“Independent- samples T Test”对话框
从对话框左侧的变量列表中选“时间”，进入“Test Variable(s)”框，选择变量“方法”，进入“Grouping Variable”框
如图 4-7 所示图 4-7第二步：点击“Define Groups”按钮弹出“Define Groups”定义框，在 Group 1 中输入“1”，在 Group 2 中输入“2”
第三步：点击“Options” 按钮弹出“Confidence Interval”定义框，在“Confidence Interval”框中输入“95”，点击“Continue”第四步：单击“OK”按钮，得到输出结果
Independent
