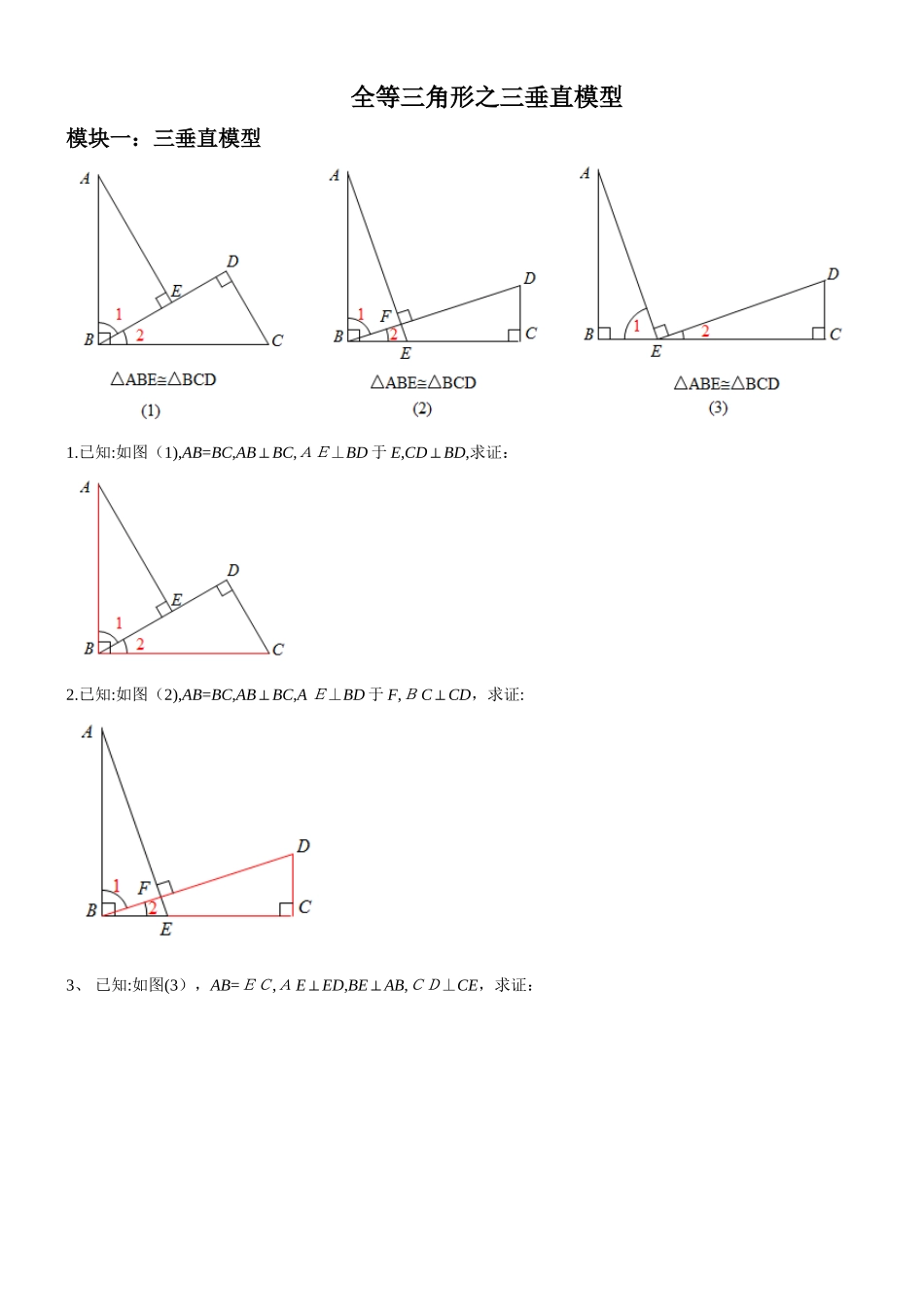
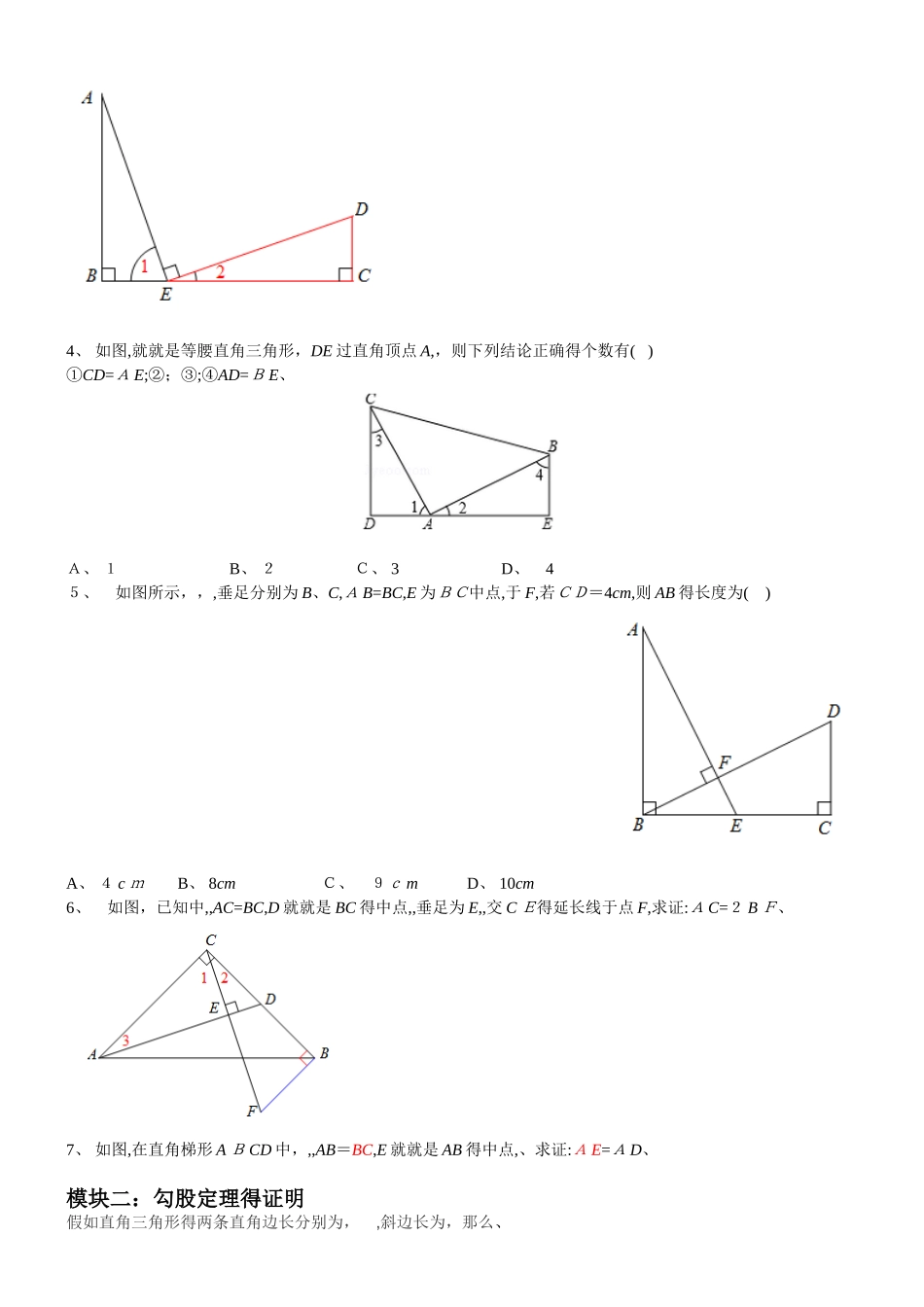
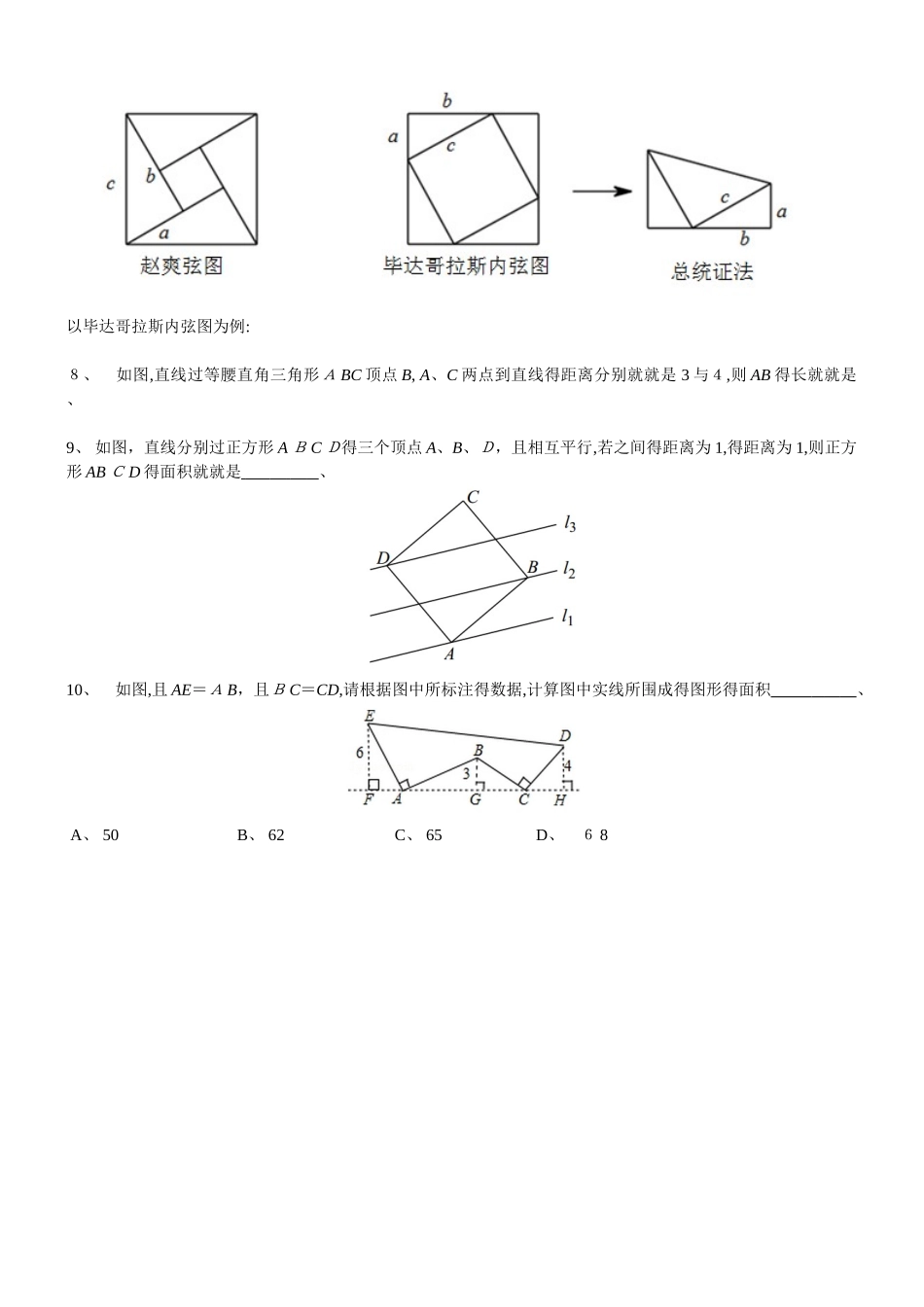
全等三角形之三垂直模型模块一:三垂直模型1.已知:如图(1),AB=BC,AB⊥BC,AE⊥BD 于 E,CD⊥BD,求证:2.已知:如图(2),AB=BC,AB⊥BC,A E⊥BD 于 F,B C⊥CD,求证:3、 已知:如图(3),AB=EC,A E⊥ED,BE⊥AB,CD⊥CE,求证:4、 如图,就就是等腰直角三角形,DE 过直角顶点 A,,则下列结论正确得个数有( )①CD=A E;②;③;④AD=B E、A、 1 B、 2 C、 3 D、 45、 如图所示,,,垂足分别为 B、C,A B=BC,E 为BC中点,于 F,若CD=4cm,则 AB 得长度为( )A、 4 c m B、 8cm C、 9c m D、 10cm 6、 如图,已知中,,AC=BC,D 就就是 BC 得中点,,垂足为 E,,交 C E得延长线于点 F,求证:A C=2 B F、 7、 如图,在直角梯形 A B CD 中,,,AB=BC,E 就就是 AB 得中点,、求证:A E=A D、模块二:勾股定理得证明假如直角三角形得两条直角边长分别为, ,斜边长为,那么、以毕达哥拉斯内弦图为例:8、 如图,直线过等腰直角三角形A BC 顶点 B, A、C 两点到直线得距离分别就就是 3 与4,则 AB 得长就就是 、9、 如图,直线分别过正方形 A B C D得三个顶点 A、B、D,且相互平行,若之间得距离为 1,得距离为 1,则正方形 AB C D 得面积就就是 、10、 如图,且 AE=A B,且B C=CD,请根据图中所标注得数据,计算图中实线所围成得图形得面积 、 A、 50 B、 62 C、 65 D、 6 8