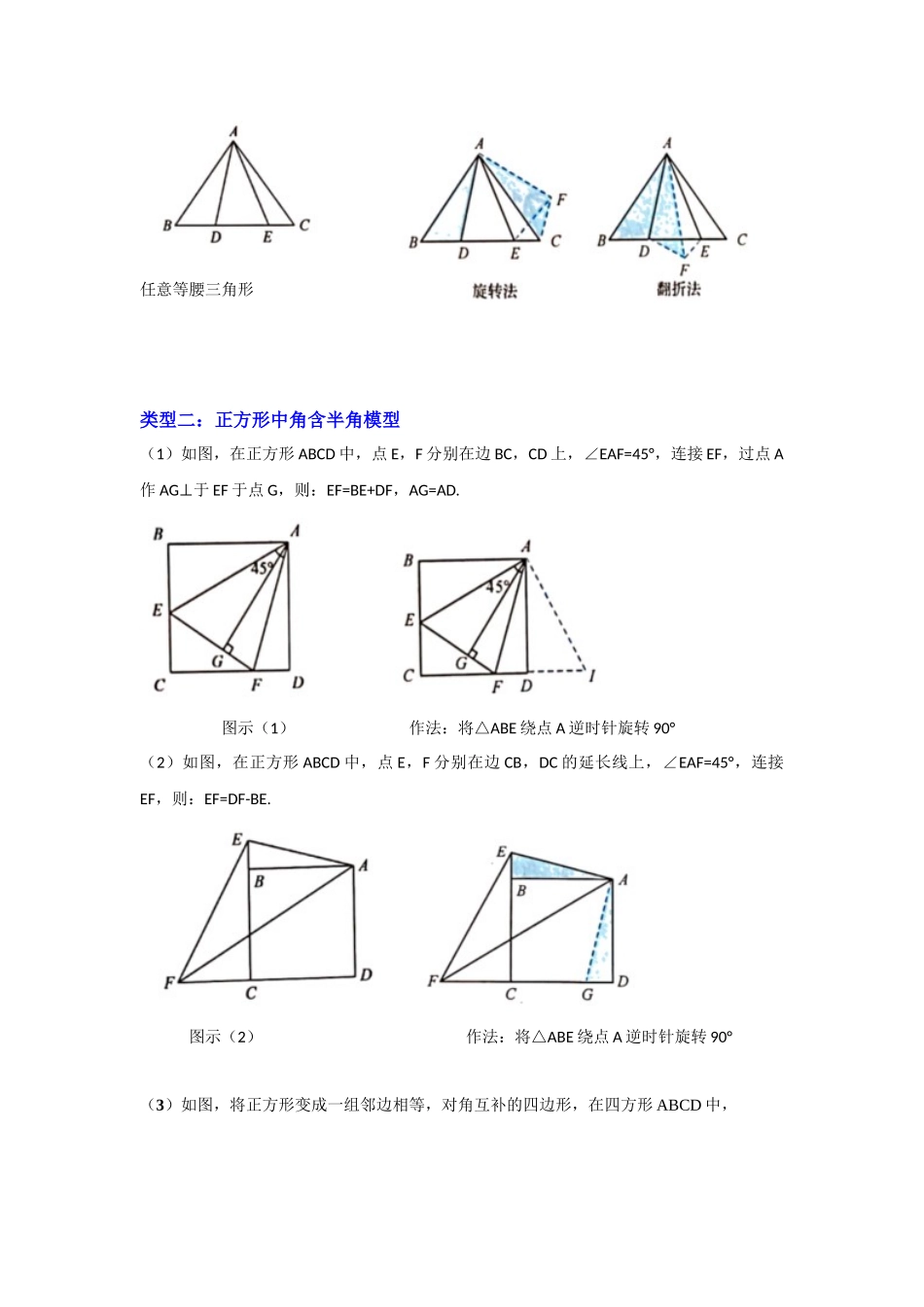
专题 06 半角模型综合应用(知识解读)【专题说明】角含半角模型,顾名思义即一个角包含着它的一半大小的角。它主要包含:等腰直角三角形角含半角模型;正方形中角含半角模型两种类型。解决类似问题的常见办法主要有两种:旋转目标三角形法和翻折目标三角形法。【方法技巧】类型一:等腰直角三角形角含半角模型(1)如图,在△ABC 中,AB=AC,∠BAC=90°,点 D,E 在 BC 上,且∠DAE=45°,则:BD+CE=DE. 旋转法 翻折法 作法 1:将△ABD 旋转 90° 作法 2:分别翻折△ABD, ACE△(2)如图,在△ABC 中,AB=AC,∠BAC=90°,点 D 在 BC 上,点 E 在 BC 延长线上,且∠DAE=45°,则:BD+CE=DE.(3)如图,将等腰直角三角形变成任意等腰三角形时,亦可以进行两种方法的操作处理..任意等腰三角形类型二:正方形中角含半角模型(1)如图,在正方形 ABCD 中,点 E,F 分别在边 BC,CD 上,∠EAF=45°,连接 EF,过点 A作 AG⊥于 EF 于点 G,则:EF=BE+DF,AG=AD. 图示(1) 作法:将△ABE 绕点 A 逆时针旋转 90°(2)如图,在正方形 ABCD 中,点 E,F 分别在边 CB,DC 的延长线上,∠EAF=45°,连接EF,则:EF=DF-BE. 图示(2) 作法:将△ABE 绕点 A 逆时针旋转 90°(3)如图,将正方形变成一组邻边相等,对角互补的四边形,在四方形 ABCD 中,AB=AD,∠BAD+C=180°∠,点 E,F 分别在边 BC,CD 上,∠EAF=BAD∠,连接EF,则:EF=BE+DF.图示(3) 作法:将△ABE 绕点 A 逆时针旋转∠BAD 的大小类型三:等边三角形中 120°含 60°的半角模型 作辅助线:延长 FC 到 G,使得 CG=BE,连接 DG结论:▲DEFDGF≌▲;EF=BE+CF【典例分析】【类型一:等腰直角三角形角含半角模型】【典例 1】如图,四边形 ABCD 中,∠A=∠BCD=90°,BC=CD,若将△ABC 绕着点 C 逆时针旋转 90°得△EDC.(1)求证:∠ADC+∠CDE=180°;(2)若 AB=3cm,AC=,求 AD 的长;(3)在(2)的条件下,求四边形 ABCD 的周长和面积.【变式 1-1】如图,Rt△ABC 中,∠BAC=90°,AB=AC,D、E 为 BC 边上两点,∠DAE=45°,过 A 点作 AF⊥AE,且 AF=AE,连接 DF、BF.下列结论:①△ABF△ACE,② AD 平分∠EDF;③若 BD=4,CE=3,则 AB=6;④若 AB=BE,S△ABD=,其中正确的个数有( )A.1 个B.2 个C.3 个D.4 个【变式 1-2】如图,等腰直角三角形 ABC ...