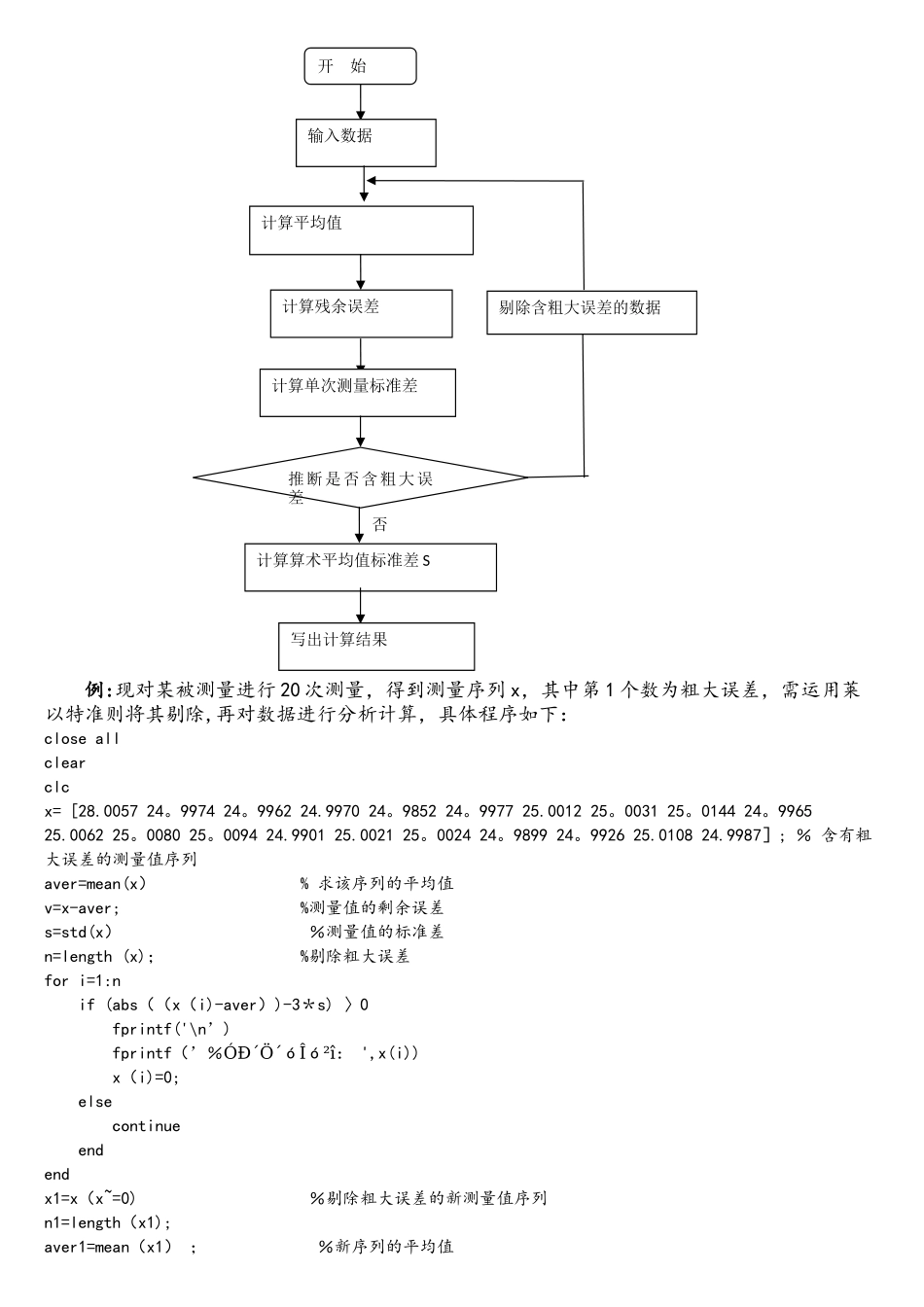
MATLAB 在测量误差分析中的应用在技术测量中,根据误差的特点与性质,误差可分为:系统误差,粗大误差和随机误差。在假定不含有系统误差的情况下,可借助MATLAB对测量数据进行处理,使处理过程快速、结果可靠。处理测量数据的处理过程如下:(1)按测量的先后顺序记录下个测量值;(2)计算算术平均值;(3)计算残余误差 ;(4)校核算术平均值及残余误差;(5)推断是否有粗大误差,若有,剔除;(6)计算单次测量的标准差;(7)计算算术平均值的标准差:(8)计算算术平均值的极限误差;(9)列出测量结果。误差处理时常用的 MATLAB 函数序号函数名调用格式作用1 absB=abs(a)求绝对值2 sqrtB=sqrt(a)对向量中的值依次开平方3 meanb=mean(a)求平均值4 stdb=std(a)求标准差5 cova=cov(x,y)求协方差6 normrndW=normrnd(,, , )生成正态分布的向量7 normstat[E,D]=(mu,sigma)计算正态分布的期望与方差8 normfit[muhat,sigmut,muci,sigmaci]= normfit(X,Alpha)已知数据符合正态分布,对参数进行点估量和区间估量其算法流程图如下:例:现对某被测量进行 20 次测量,得到测量序列 x,其中第 1 个数为粗大误差,需运用莱以特准则将其剔除,再对数据进行分析计算,具体程序如下:close allclearclcx= [28.0057 24。9974 24。9962 24.9970 24。9852 24。9977 25.0012 25。0031 25。0144 24。9965 25.0062 25。0080 25。0094 24.9901 25.0021 25。0024 24。9899 24。9926 25.0108 24.9987]; % 含有粗大误差的测量值序列aver=mean(x) % 求该序列的平均值v=x-aver; %测量值的剩余误差 s=std(x) %测量值的标准差n=length (x); %剔除粗大误差for i=1:n if (abs((x(i)-aver))-3*s) 〉0 fprintf('\n’) fprintf(’%ó óÓдִβî: ',x(i)) x(i)=0; else continue end endx1=x(x~=0) %剔除粗大误差的新测量值序列n1=length(x1);aver1=mean(x1) ; %新序列的平均值开 始输入数据计算平均值计算残余误差计算单次测量标准差推断是否含粗大误差计算算术平均值标准差 S写出计算结果否剔除含粗大误差的数据h1=std(x1);aver1 %测量值的最佳近似值s1=h1/sqrt(n1) %算术平均值的标准差运行结果:aver = 25。1502s = 0。6721x1 = 24.9974 24.9962 24.9970 24.9852 24。9977 25。0012 25.0031 25。0144 4。9965 25.0062 25.0080 25.0094 24.9901 25.0021 25。0024 24.9899 24.9926 25.0108 24。9987 %新序列aver1 = 24。9999s1 = 0。0018由结果可知:通过上述方法处理测量数据可剔除粗大误差,极大减小测量结果的标准差,且处理过程快速、结果可靠.