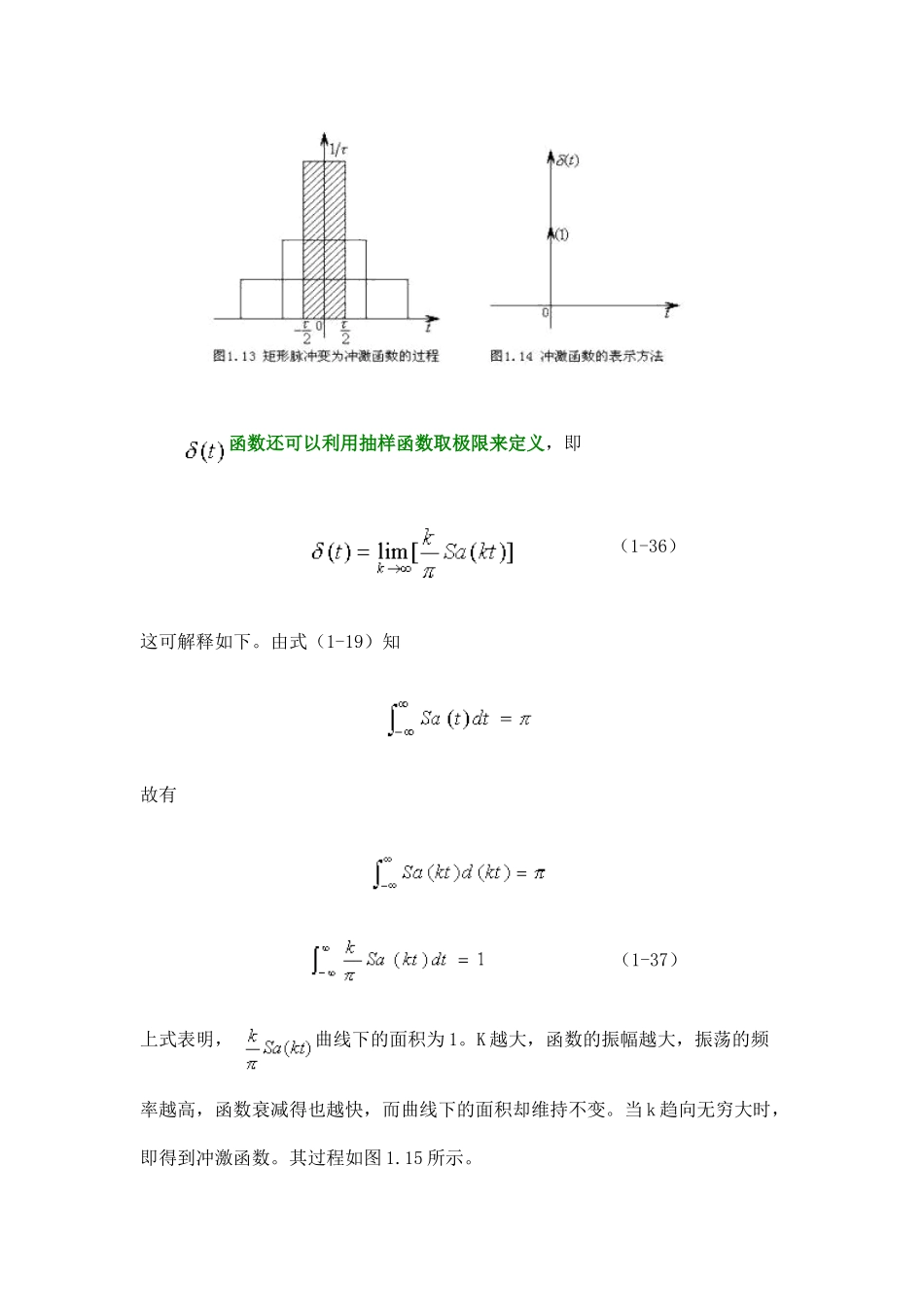
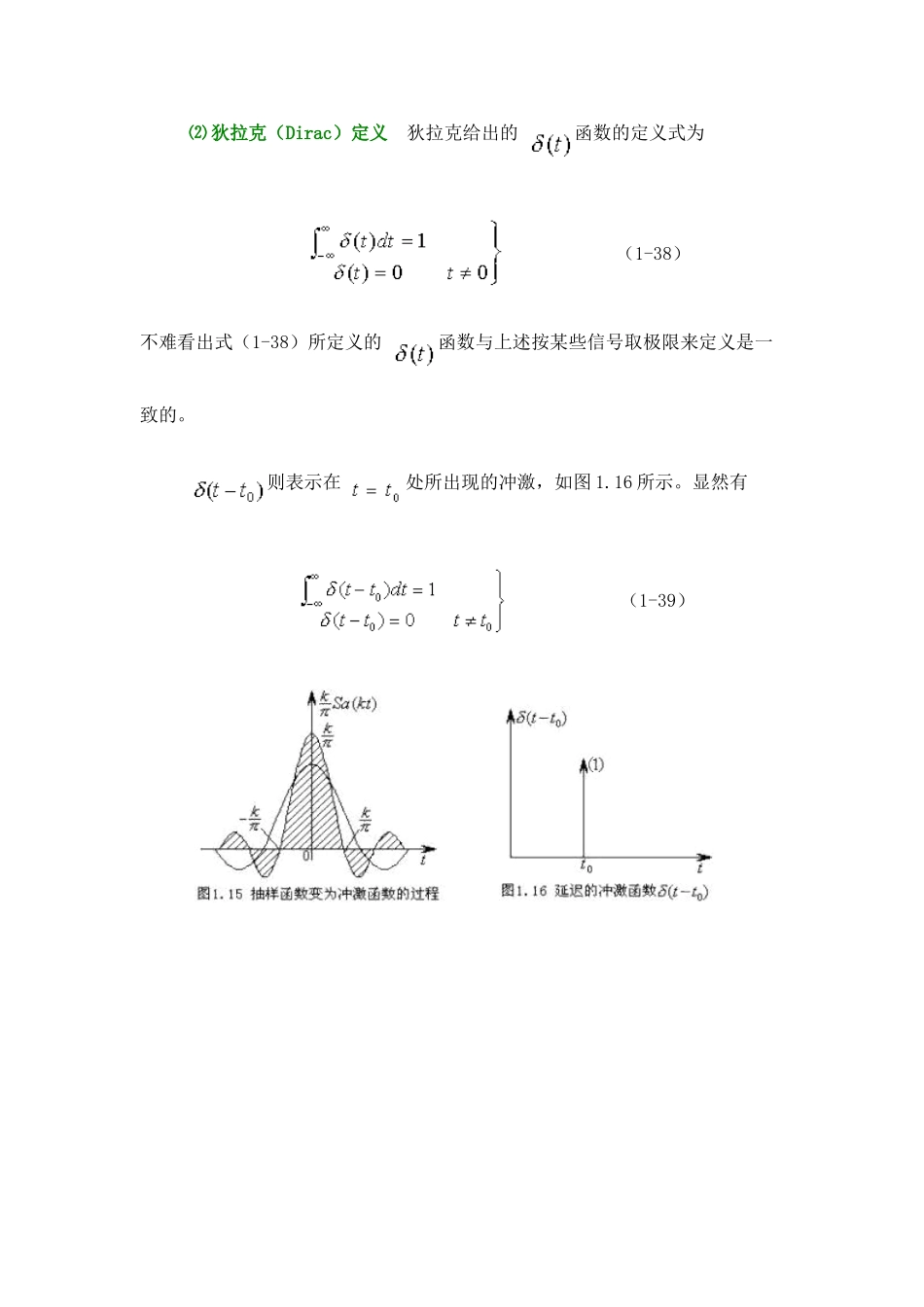
冲击函数 函数有几种不同的定义方式,其中根据广义函数(或称分配函数)来定义的,是严格的数学定义,因篇幅所限,本课程将不予讨论。本课程介绍另外两种定义。 ⑴ 从某些函数的极限来定义 函数 单位冲激函数可视为幅度与脉宽 的乘积(矩形面积)为 1 个单位的矩形脉冲,当 趋于零时脉冲幅度趋于无穷大的极限情况,即 (1-35) 图 1.13 表示了 时,上述矩形脉冲的变化过程。 冲激函数常用图 1.14 所示带箭头的线段来表示。 函数只在 t=0 处有“冲激”,而在 t 轴上其它各点取值为零。假如矩形面积为 1,则在带箭头的线段旁注上(1),表明冲激强度为单位值。假如在图形上将(E)注于箭头旁,则表示冲激强度为 E 被单位值的 函数。 函数还可以利用抽样函数取极限来定义,即 (1-36) 这可解释如下。由式(1-19)知 故有 (1-37) 上式表明, 曲线下的面积为 1。K 越大,函数的振幅越大,振荡的频率越高,函数衰减得也越快,而曲线下的面积却维持不变。当 k 趋向无穷大时,即得到冲激函数。其过程如图 1.15 所示。⑵ 狄拉克(Dirac)定义 狄拉克给出的 函数的定义式为 (1-38) 不难看出式(1-38)所定义的 函数与上述按某些信号取极限来定义是一致的。 则表示在 处所出现的冲激,如图 1.16 所示。显然有 (1-39)