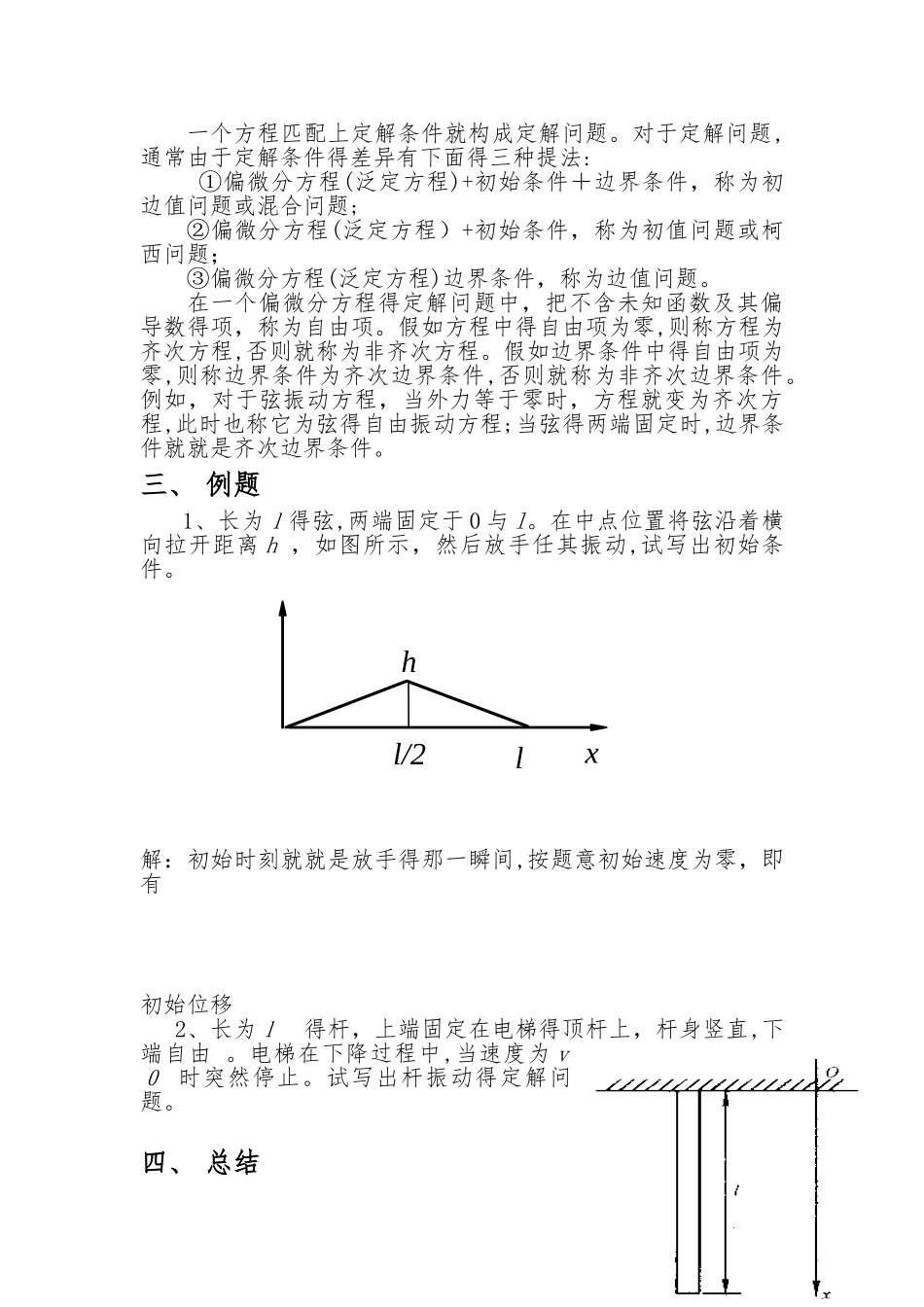
定解条件与定解问题含有未知函数得偏导数得方程叫偏微分方程,常微分方程可以瞧成就是特别得偏微分方程。方程得分数就是 1 得称为方程式,个数多于 1 得叫做方程组。方程(组)中出现得未知函数得最高阶偏导数得阶数称为方程(组)得阶数。假如方程(组)中得项关于未知函数及其各阶偏导数得整体来讲就是线性得,就称方程(组)为线性得,否则就称为非线性得。非线性又分为半线性、拟线性与完全非线性。一、 定解条件给定一个常微分方程,有通解与特解得概念。通解只要求满足方程,即满足某种物理定律,而不能完全确定一个物理状态。特解除了要求满足方程还要满足给定得外加(特别)条件。对偏微分方程也就是如此,换句话说,只有偏微分方程还不足以确定一个物理量随空间与时间得变化规律,因为在特定情况下这个物理量还与它得初始状态与它在边界受到得约束有关。描述初始时刻得物理状态与边界得约束情况,在数学上分别称为初始条件(或初值条件)与边界条件(或边值条件),她们统称为定解条件。初始条件:能够用来说明某一具体物理现象初始状态得条件,即描述物理过程初始状态得数学条件。边界条件:能够用来说明某一具体物理现象边界上得约束情况得条件,即描述物理过程边界状态得数学条件。定解条件:初始条件与边界条件得统称。非稳态问题:定解条件包括初始条件与边界条件。稳态问题:定解条件为边界条件。1、弦振动方程 ( )初始条件就是指初始时刻()弦得位移与速度。若以, 分别表示弦上任意点得初始位移与初始速度,则初始条件为: 边界条件就是指弦在两端点得约束情况,一般有三种类型。(1)第一类边界条件(狄利克雷(Dirichlet)边界条件):已知端点处弦得位移就是,则边界条件为: 或 当时,表示在该点处弦就是固定得。(2)第二类边界条件(诺伊曼(N e u m ann)边界条件):已知端点弦所受得垂直于弦线得外力或,则边界条件为: 或 当,表示弦在端点处自由滑动。(3)第三类边界条件(混合边界条件或罗宾(Ro bi n)边界条件:已知端点处弦得位移与所受得垂直于弦线得外力得与:或,其中表示两端支承得弹性系数,当时,表示弦在该端点处被固定在一个弹性支承上。2、热传导方程(初始条件就是指初始时刻物体内得温度分布情况。式中 φ( x, y, z )为已知函数,表示温度在初始时刻得分布。边界条件就是指边界上温度受周围介质得影响情况,可分为三种。(1)第一类边界条件:介质表面温度已知 式中,p 为边界面上得点。 (2)第二类边界条件:通过介质表面单位面积...