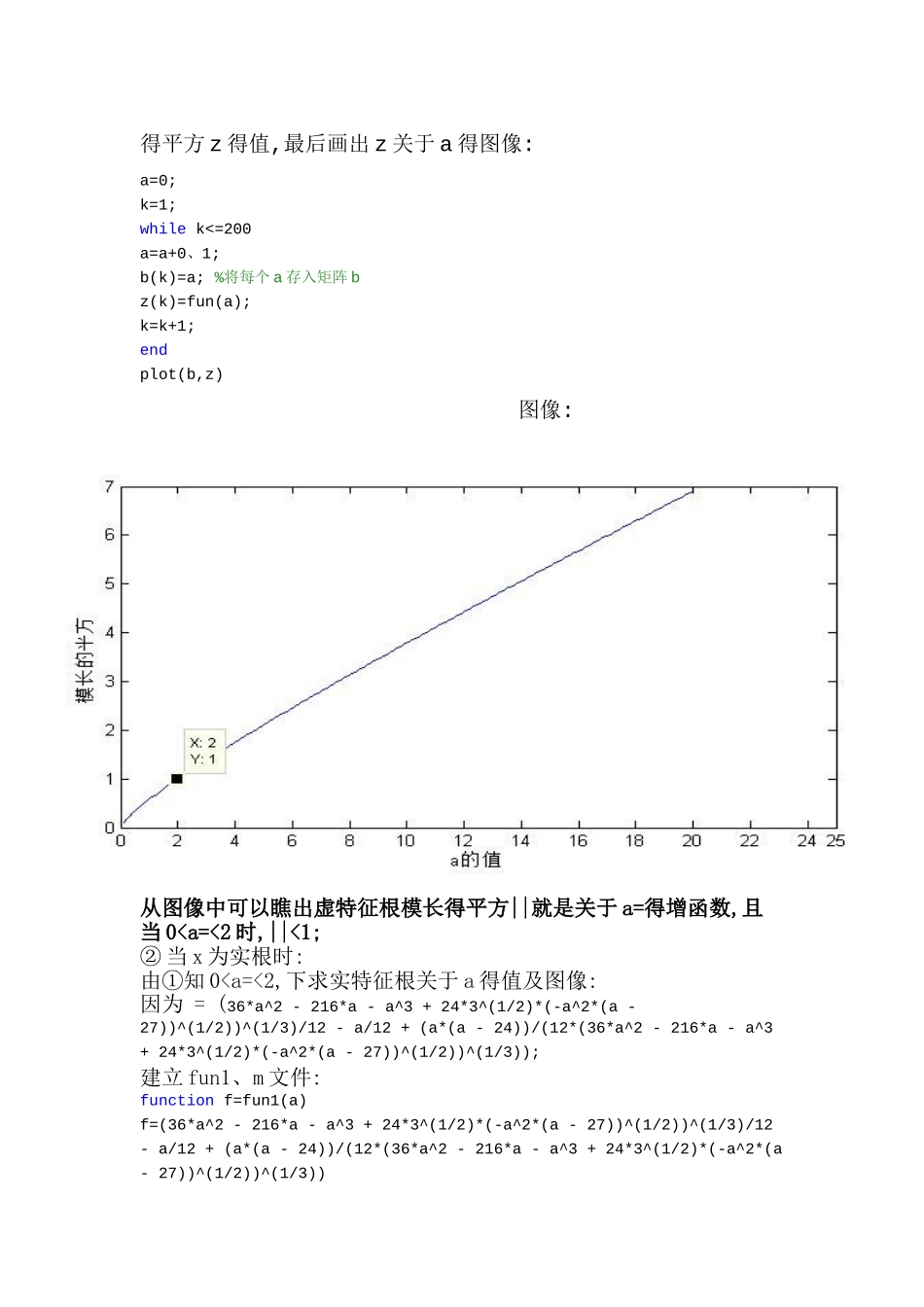
对于 6、4 节蛛网模型讨论下列问题:(1)因为一个时段上市得商品不能立即售完,其数量也会影响到下一时段得价格,所以第 k+1 时段得价格由第 k+1 与第 k 时段得数量与决定。假如设仍只取决于,给出稳定平衡得条件,并与 6、4 得结果进行比较。(2)若除了由与决定之外,也由前两个时段得价格与决定,试分析稳定平衡得条件就是否还会放宽。解:(1)设由与得平均值决定,即价格函数表示为:则 消去 y, 得到 ,k=1,2,…、 该方程得特征方程为与 6、4 节中 时得特征方程一样,所以 0<<2, 即为点得稳定条件。(2)设 ,则有 消去 y,得到 该方程得特征方程为 令=x,=a , 即求解三次方程 得根在 matlab 中输入以下代码求解方程得根 x: syms x a solve(4*x^3+a*x^2+2*a*x+a==0,x)解得 = (36*a^2 - 216*a - a^3 + 24*3^(1/2)*(-a^2*(a - 27))^(1/2))^(1/3)/12 - a/12 + (a*(a - 24))/(12*(36*a^2 - 216*a - a^3 + 24*3^(1/2)*(-a^2*(a - 27))^(1/2))^(1/3)); = -(2*a*(36*a^2 - 216*a - a^3 + 24*3^(1/2)*(-a^2*(a - 27))^(1/2))^(1/3) - 3^(1/2)*a*24*i - 3^(1/2)*(36*a^2 - 216*a - a^3 + 24*3^(1/2)*(-a^2*(a - 27))^(1/2))^(2/3)*i - 24*a + 3^(1/2)*a^2*i + (36*a^2 - 216*a - a^3 + 24*3^(1/2)*(-a^2*(a - 27))^(1/2))^(2/3) + a^2)/(24*(36*a^2 - 216*a - a^3 + 24*3^(1/2)*(-a^2*(a - 27))^(1/2))^(1/3)); =-(2*a*(36*a^2 - 216*a - a^3 + 24*3^(1/2)*(-a^2*(a - 27))^(1/2))^(1/3) + 3^(1/2)*a*24*i + 3^(1/2)*(36*a^2 - 216*a - a^3 + 24*3^(1/2)*(-a^2*(a - 27))^(1/2))^(2/3)*i - 24*a - 3^(1/2)*a^2*i + (36*a^2 - 216*a - a^3 + 24*3^(1/2)*(-a^2*(a - 27))^(1/2))^(2/3) + a^2)/(24*(36*a^2 - 216*a - a^3 + 24*3^(1/2)*(-a^2*(a - 27))^(1/2))^(1/3));其中为实根,与为一对共轭虚根。①x 为虚根时:易知||=*=*,在 matlab 中输入代码: f=x2*conj(x2) %求特征根模长得平方可得||=f=(a/12 - (3^(1/2)*((- a^2/144 + a/6)/(((a/6 - a^2/144)^3 + (a^3/1728 - a^2/48 + a/8)^2)^(1/2) - a/8 + a^2/48 - a^3/1728)^(1/3) + (((- a^2/144 + a/6)^3 + (a^3/1728 - a^2/48 + a/8)^2)^(1/2) - a/8 + a^2/48 - a^3/1728)^(1/3))*i)/2 - (- a^2/144 + a/6)/(2*((...