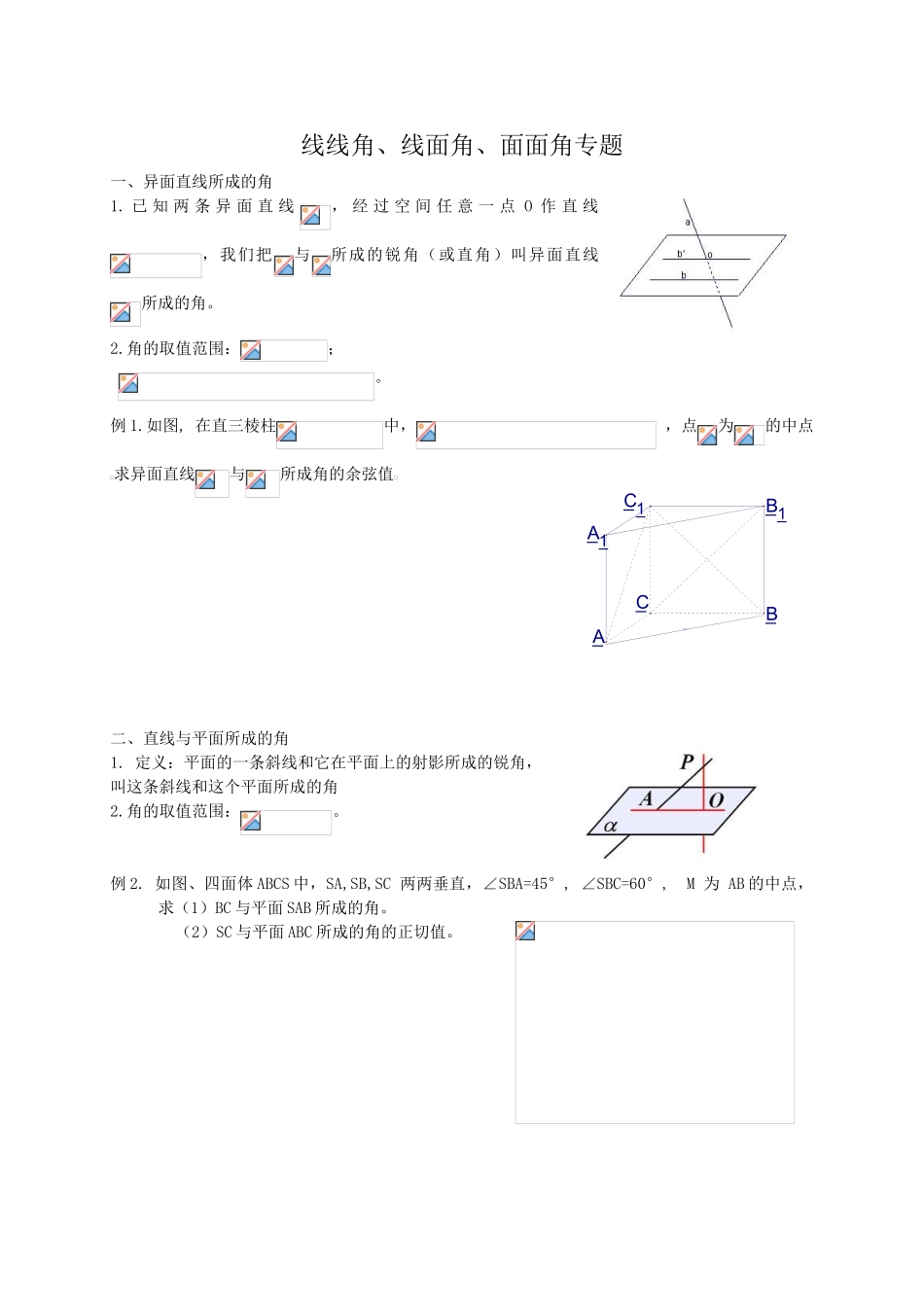
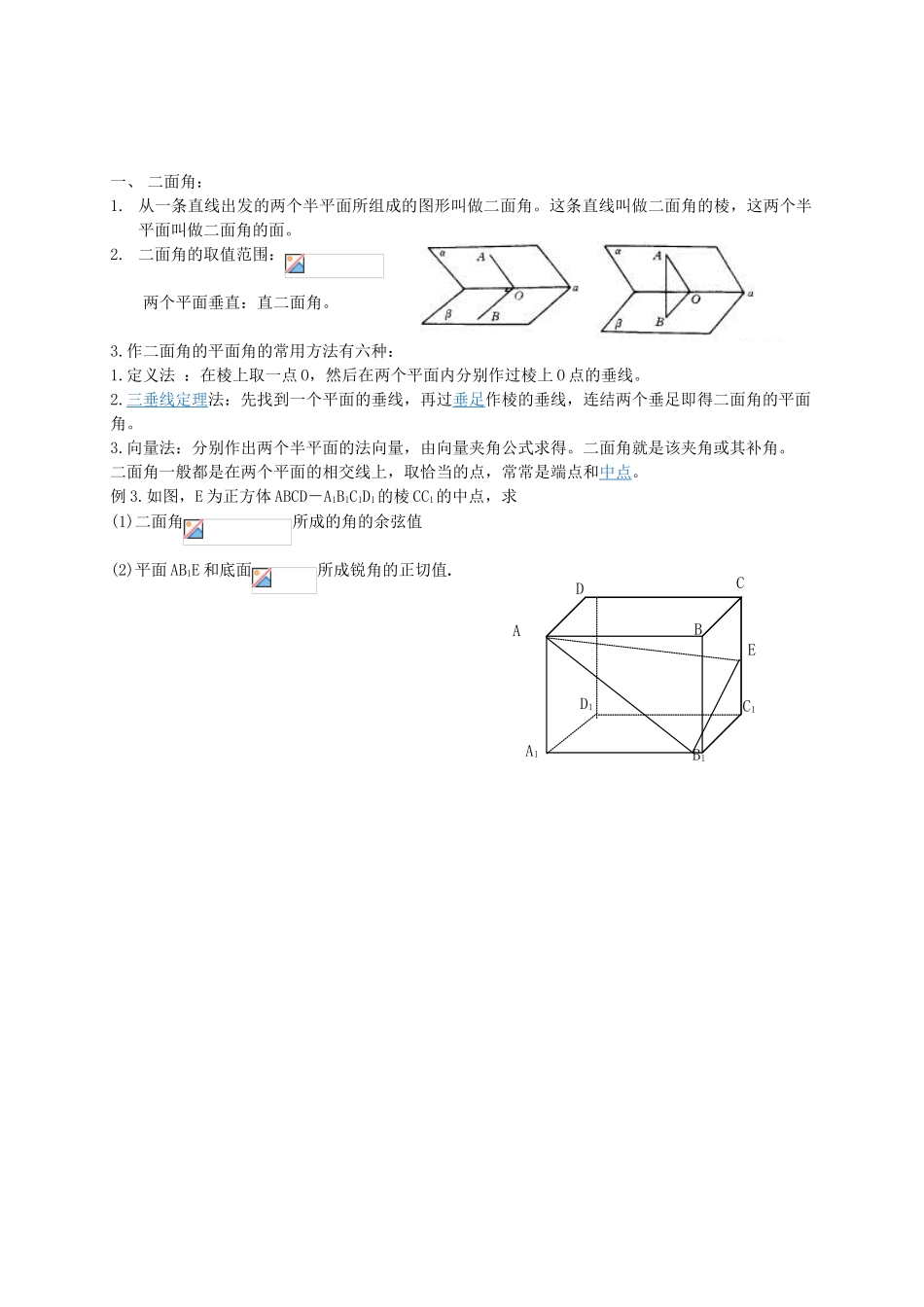
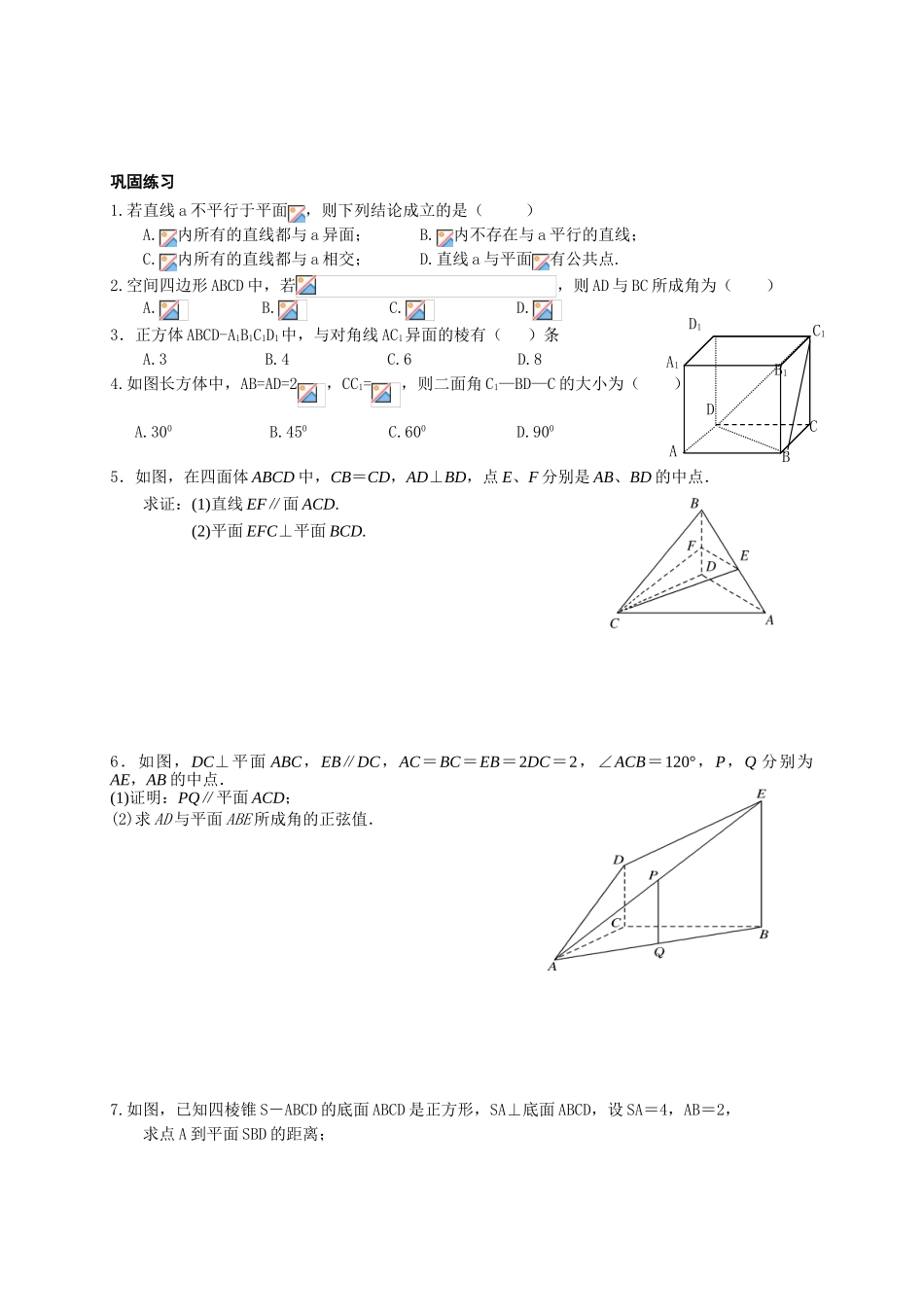
线线角、线面角、面面角专题一、异面直线所成的角1. 已 知 两 条 异 面 直 线, 经 过 空 间 任 意 一 点 O 作 直 线,我们把与所成的锐角(或直角)叫异面直线所成的角。2.角的取值范围:;。例 1.如图, 在直三棱柱中, ,点为的中点求异面直线与所成角的余弦值二、直线与平面所成的角1. 定义:平面的一条斜线和它在平面上的射影所成的锐角,叫这条斜线和这个平面所成的角2.角的取值范围:。例 2. 如图、四面体 ABCS 中,SA,SB,SC 两两垂直,∠SBA=45°, ∠SBC=60°, M 为 AB 的中点,求(1)BC 与平面 SAB 所成的角。(2)SC 与平面 ABC 所成的角的正切值。_C_1_B_1_A_1_A_B_C一、 二面角:1. 从一条直线出发的两个半平面所组成的图形叫做二面角。这条直线叫做二面角的棱,这两个半平面叫做二面角的面。 2. 二面角的取值范围: 两个平面垂直:直二面角。3.作二面角的平面角的常用方法有六种:1.定义法 :在棱上取一点 O,然后在两个平面内分别作过棱上 O 点的垂线。2.三垂线定理法:先找到一个平面的垂线,再过垂足作棱的垂线,连结两个垂足即得二面角的平面角。3.向量法:分别作出两个半平面的法向量,由向量夹角公式求得。二面角就是该夹角或其补角。二面角一般都是在两个平面的相交线上,取恰当的点,常常是端点和中点。例 3.如图,E 为正方体 ABCD-A1B1C1D1的棱 CC1的中点,求(1)二面角所成的角的余弦值(2)平面 AB1E 和底面所成锐角的正切值.A1D1B1C1EDBCA巩固练习1.若直线 a 不平行于平面,则下列结论成立的是( )A.内所有的直线都与 a 异面; B.内不存在与 a 平行的直线;C.内所有的直线都与 a 相交; D.直线 a 与平面有公共点.2.空间四边形 ABCD 中,若,则 AD 与 BC 所成角为( )A. B. C. D.3.正方体 ABCD-A1B1C1D1中,与对角线 AC1异面的棱有( )条 A.3 B.4 C.6 D.8 4.如图长方体中,AB=AD=2,CC1=,则二面角 C1—BD—C 的大小为( ) A.300 B.450 C.600 D.9005.如图,在四面体 ABCD 中,CB=CD,AD⊥BD,点 E、F 分别是 AB、BD 的中点.求证:(1)直线 EF∥面 ACD. (2)平面 EFC⊥平面 BCD.6.如图,DC⊥平面 ABC,EB∥DC,AC=BC=EB=2DC=2,∠ACB=120°,P,Q 分别为AE,AB 的中点.(1)证明:PQ∥平面 ACD;(2)求 AD 与平面 ABE 所成角的正弦值.7.如图,已知四棱锥 S-ABCD 的底面 ABCD 是正方形,SA⊥底面 ABCD,设 SA=4,AB=2,求点 A 到平面 SBD 的距离;ABCDA1B1C1D1