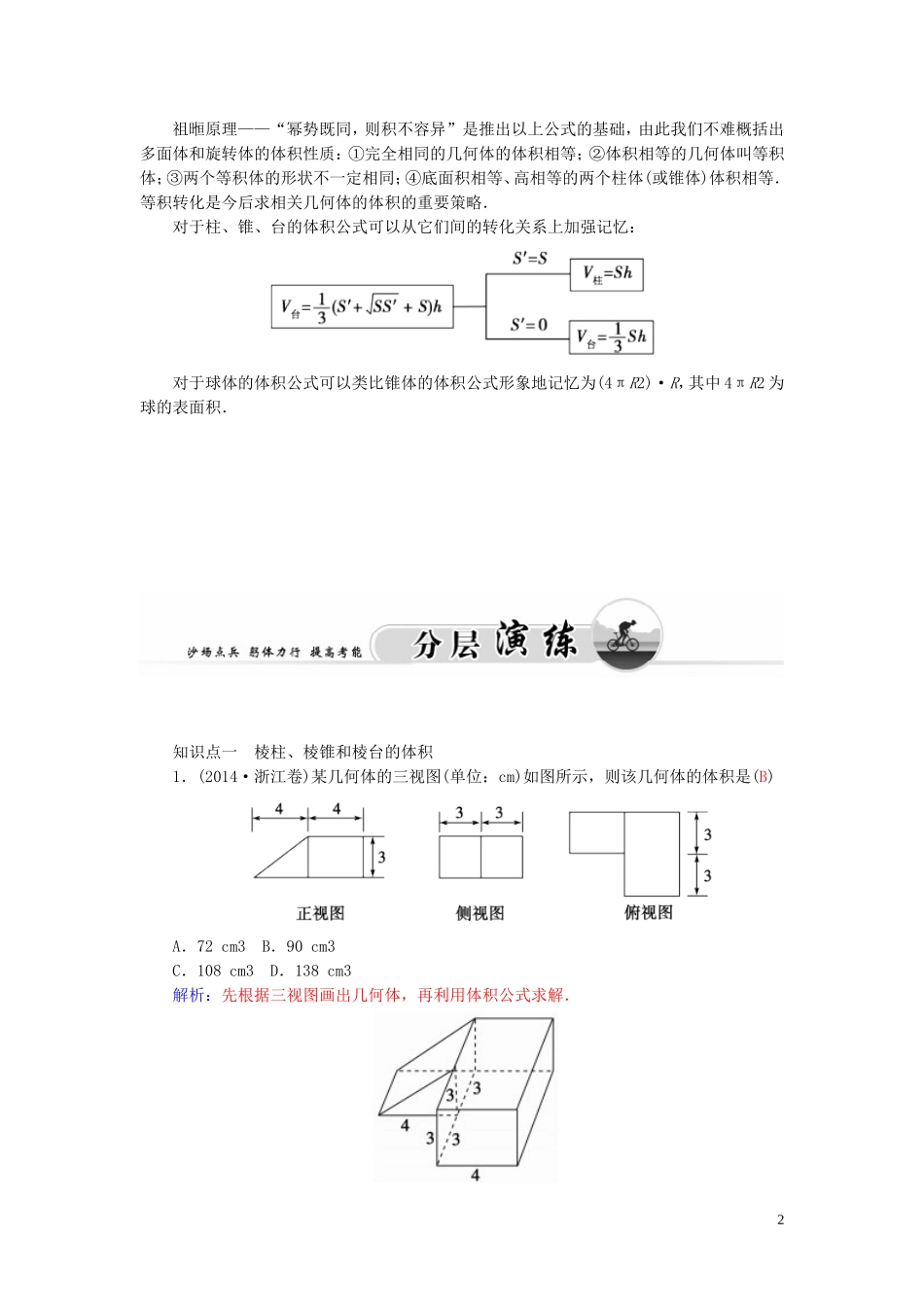
1.3.2 空间几何体的体积空间几何体的度量是几何研究的重要内容之一,在生活中有着重要应用的不仅是度量几何体的表面积还有度量体积.如下图,在一个圆锥形的空杯子上面放着一个半球形的冰淇淋,如果冰淇淋融化了,会溢出杯子吗?在实际操作中如何解答呢?1.几何体的体积是几何体占有空间部分的大小,其主要性质有:①完全相同的几何体的体积相等;②体积相等的几何体叫等积体;③两个等积体的形状不一定相同;④底面积相等、高相等的两个柱体(或锥体)体积相等.2.①棱柱的体积公式:V 棱柱=Sh(S 为底面面积,h 为柱体的高);② 棱锥的体积公式:V 棱锥=Sh(S 为底面面积,h 为棱锥的高);③ 棱台的体积公式:V 棱台=( S ′ ++ S ) h (S′、S 为两底面面积,h 为棱台的高).3.①圆柱的体积公式:V 圆柱=Sh=π R 2 h (R 为底面圆的半径,h 为圆柱的高);② 圆锥的体积公式:V 圆锥=Sh=π R 2 h (R 为底面圆的半径,h 为圆锥的高);③ 圆台的体积公式:V 圆台=( S ′ ++ S ) h =π ( r 2 + rR + R 2 ) h (r、R 为两底面圆半径,h为圆台的高).4.球的体积公式:V 球=π R 3 (R 为球半径),表面积公式为:S 球=4 π R 2 .棱体、锥体、台体和球的体积公式① 柱体的体积公式:V 柱体=Sh(S 为底面面积,h 为柱体的高);② 锥体的体积公式:V 锥体=Sh(S 为底面面积,h 为锥体的高);③ 台体的体积公式:V 台体=(S′++S)h(S′、S 为两底面面积,h 为台体的高);④ 球体的体积公式:V 球=πR3(R 为球半径).1祖暅原理——“幂势既同,则积不容异”是推出以上公式的基础,由此我们不难概括出多面体和旋转体的体积性质:①完全相同的几何体的体积相等;②体积相等的几何体叫等积体;③两个等积体的形状不一定相同;④底面积相等、高相等的两个柱体(或锥体)体积相等.等积转化是今后求相关几何体的体积的重要策略.对于柱、锥、台的体积公式可以从它们间的转化关系上加强记忆:对于球体的体积公式可以类比锥体的体积公式形象地记忆为(4πR2)·R,其中 4πR2 为球的表面积. 知识点一 棱柱、棱锥和棱台的体积1.(2014·浙江卷)某几何体的三视图(单位:cm)如图所示,则该几何体的体积是(B)A.72 cm3 B.90 cm3C.108 cm3 D.138 cm3解析:先根据三视图画出几何体,再利用体积公式求解.2该几何体为一个组合体,左侧为三棱柱,右侧为长方体...