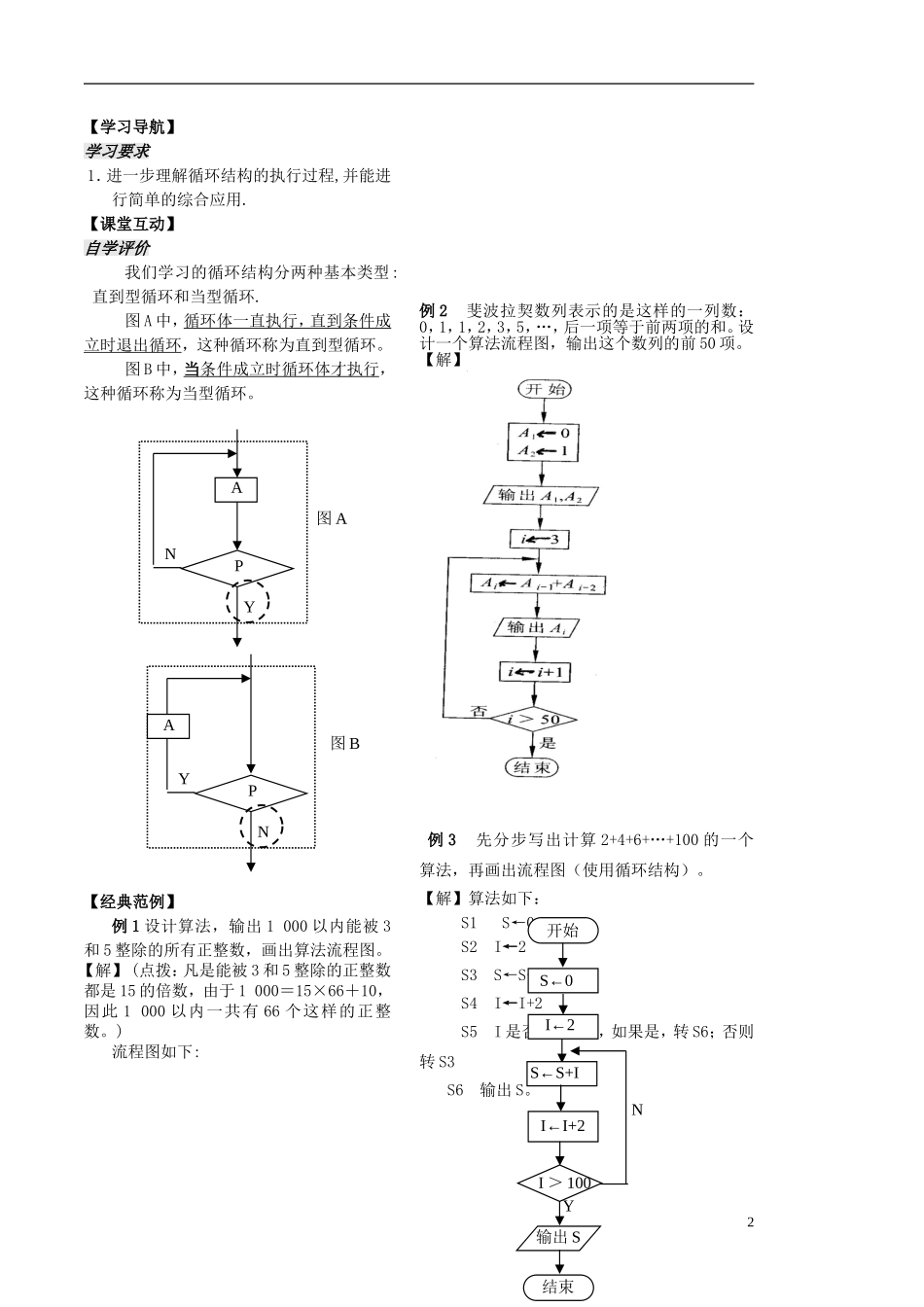
第 5 课时 5.2 流程图1【学习导航】 学习要求 1.进一步理解循环结构的执行过程,并能进行简单的综合应用.【课堂互动】自学评价我们学习的循环结构分两种基本类型: 直到型循环和当型循环.图 A 中,循环体一直执行,直到条件成立时退出循环,这种循环称为直到型循环。图 B 中,当 条件成立时循环体才执行 ,这种循环称为当型循环。【经典范例】例 1 设计算法,输出 1 000 以内能被 3和 5 整除的所有正整数,画出算法流程图。【解】 (点拨:凡是能被 3 和 5 整除的正整数都是 15 的倍数,由于 1 000=15×66+10,因此 1 000 以内一共有 66 个这样的正整数。)流程图如下:例 2 斐波拉契数列表示的是这样的一列数:0,1,1,2,3,5,…,后一项等于前两项的和。设计一个算法流程图,输出这个数列的前 50 项。【解】例 3 先分步写出计算 2+4+6+…+100 的一个算法,再画出流程图(使用循环结构)。【解】算法如下:S1 S←0S2 I←2S3 S←S+IS4 I←I+2S5 I 是否大于 100,如果是,转 S6;否则转 S3S6 输出 S。YPAN图 ANPY图 BA开始S←0I←2S←S+II←I+2I > 100YN输出 S结束2【追踪训练】1.下图给出的是计算的值的一个程序框图,其中判断框内应填入的条件是( B )A. i>100 B. i≤100 C. i>50 D. i≤50 N S←S+1/I I←I+2 输出 S 结束 I←2 Y 开始 S←0 2.请观察给出的流程图(如下图),这是一个求和算法的流程图,请运行几步看一看,指出该循环结构的循环体、循环变量和循环的终止条件。【解】s,i 为循环变量;终止条件为 i>43.设计算法流程图,输出 200 以内除以 3 余 1 的正整数。解:流程图如下:(将“=”换成“←”) 开始 n=1 输出 n n=n+3 n>20000 结束 YN3